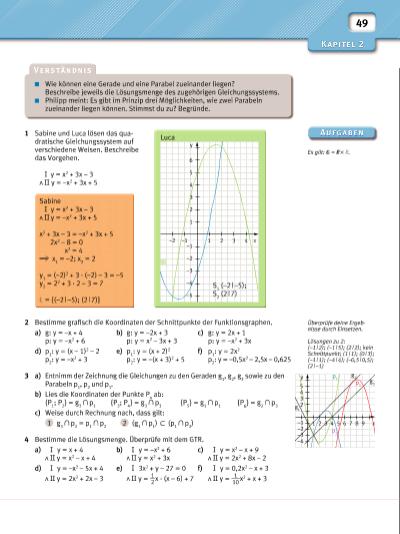
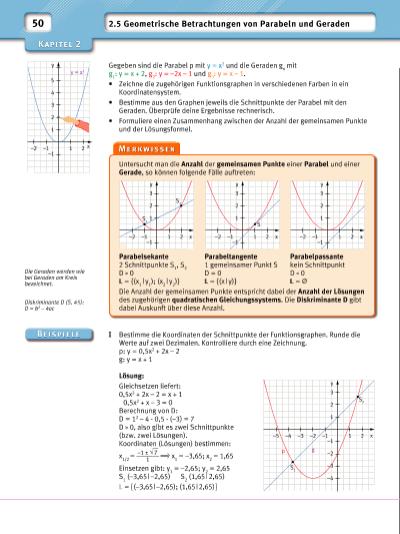
50 2.5 Geometrische Betrachtungen von Parabeln und Geraden Gegeben sind die Parabel p mit y = x2 und die Geraden g n mit g 1 : y = x + 2, g 2 : y = –2x – 1 und g 3 : y = x – 1. • Zeichne die zugehörigen Funktionsgraphen in verschiedenen Farben in ein Koordinatensystem. • Bestimme aus den Graphen jeweils die Schnittpunkte der Parabel mit den Geraden. Überprüfe deine Ergebnisse rechnerisch. • Formuliere einen Zusammenhang zwischen der Anzahl der gemeinsamen Punkte und der Lösungsformel. Untersucht man die Anzahl der gemeinsamen Punkte einer Parabel und einer Gerade, so können folgende Fälle auftreten: Parabelsekante Parabeltangente Parabelpassante 2 Schnittpunkte S 1 , S 2 1 gemeinsamer Punkt S kein Schnittpunkt D 0 D = 0 D 0 = {(x 1 | y 1 ); (x 2 | y 2 )} = {(x | y)} = Die Anzahl der gemeinsamen Punkte entspricht dabei der Anzahl der Lösungen des zugehörigen quadratischen Gleichungssystems. Die Diskriminante D gibt dabei Auskunft über diese Anzahl. Diskriminante D (S. 45): D = b2 – 4ac 1 1 2 3 4 –1 5 y 2–2 –1 x y = x2 Die Geraden werden wie bei Geraden am Kreis bezeichnet. I Bestimme die Koordinaten der Schnittpunkte der Funktionsgraphen. Runde die Werte auf zwei Dezimalen. Kontrolliere durch eine Zeichnung. p: y = 0,5x2 + 2x – 2 g: y = x + 1 Lösung: Gleichsetzen liefert: 0,5x2 + 2x – 2 = x + 1 0,5x2 + x – 3 = 0 Berechnung von D: D = 12 – 4 · 0,5 · (–3) = 7 D 0, also gibt es zwei Schnittpunkte (bzw. zwei Lösungen). Koordinaten (Lösungen) bestimmen: x 1/2 = –1 ± √ __ 7 _______1 x1 = –3,65; x2 = 1,65 Einsetzen gibt: y 1 = –2,65; y 2 = 2,65 S 1 (–3,65 | –2,65) S 2 (1,65 | 2,65) = { (–3,65 | –2,65); (1,65 | 2,65) } 1 1 2 3 –1 y 2–2 –1 x S 1 S 2 1 1 2 3 –1 y –2 –3 –4 2–2–3–4–5 –1 x S 1 gp S 2 1 1 2 3 –1 y 2–2 –1 x S 1 1 2 3 –1 y 2–2 –1 x