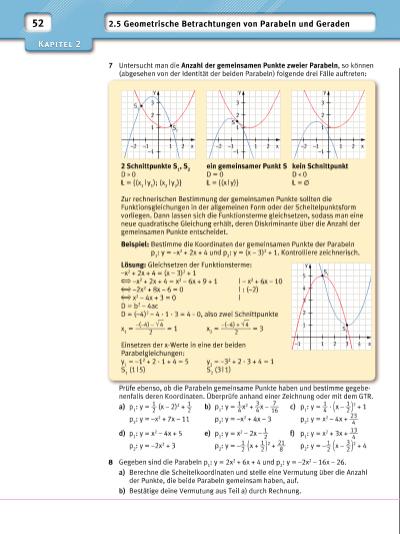
52 2.5 Geometrische Betrachtungen von Parabeln und Geraden 2 Schnittpunkte S 1 , S 2 ein gemeinsamer Punkt S kein Schnittpunkt D 0 D = 0 D 0 = {(x 1 | y 1 ); (x 2 | y 2 )} = {(x | y)} = Zur rechnerischen Bestimmung der gemeinsamen Punkte sollten die Funktionsgleichungen in der allgemeinen Form oder der Scheitelpunktsform vorliegen. Dann lassen sich die Funktionsterme gleichsetzen, sodass man eine neue quadratische Gleichung erhält, deren Diskriminante über die Anzahl der gemeinsamen Punkte entscheidet. Beispiel: Bestimme die Koordinaten der gemeinsamen Punkte der Parabeln p 1 : y = –x2 + 2x + 4 und p 2 : y = (x – 3)2 + 1. Kontrolliere zeichnerisch. Lösung: Gleichsetzen der Funktionsterme: –x2 + 2x + 4 = (x – 3)2 + 1 –x2 + 2x + 4 = x2 – 6x + 9 + 1 | – x2 + 6x – 10 –2x2 + 8x – 6 = 0 | : (–2) x2 – 4x + 3 = 0 | D = b2 – 4ac D = (–4)2 – 4 · 1 · 3 = 4 0, also zwei Schnittpunkte x 1 = –(–4) – √ __ 4 _________2 = 1 x2 = –(–4) + √ __ 4 _________2 = 3 Einsetzen der x-Werte in eine der beiden Parabelgleichungen: y 1 = –12 + 2 · 1 + 4 = 5 y 2 = –32 + 2 · 3 + 4 = 1 S 1 (1 | 5) S 2 (3 | 1) 1 1 2 3 S 1 S 2 –1 y 2–2 –1 x 1 1 S 2 3 –1 y 2–2 –1 x 1 2 1 3 –1 y 2–2 –1 x 1 2 1 3 4 5 y 2 3 4 S 2 S 1 –1 x 7 Untersucht man die Anzahl der gemeinsamen Punkte zweier Parabeln, so können (abgesehen von der Identität der beiden Parabeln) folgende drei Fälle auftreten: Prüfe ebenso, ob die Parabeln gemeinsame Punkte haben und bestimme gegebenenfalls deren Koordinaten. Überprüfe anhand einer Zeichnung oder mit dem GTR. a) p 1 : y = 1 __ 2 (x – 2) 2 + 1 __ 2 b) p1: y = 1 __ 4 x 2 + 3 __ 4 x – 7 ___ 16 c) p 1 : y = 1 __ 4 · ( x – 1 __ 2 ) 2 + 1 p 2 : y = –x2 + 7x – 11 p 2 : y = –x2 + 4x – 3 p 2 : y = x2 – 4x + 23 ___ 4 d) p 1 : y = x2 – 4x + 5 e) p 1 : y = x2 – 2x – 1 __ 2 f) p1: y = x 2 + 3x + 13 ___ 4 p 2 : y = –2x2 + 3 p 2 : y = – 1 __ 2 ( x + 1 __ 2 ) 2 + 21 ___ 8 p2: y = – 1 __ 2 ( x – 3 __ 2 ) 2 + 4 8 Gegeben sind die Parabeln p 1 : y = 2x2 + 6x + 4 und p 2 : y = –2x2 – 16x – 26. a) Berechne die Scheitelkoordinaten und stelle eine Vermutung über die Anzahl der Punkte, die beide Parabeln gemeinsam haben, auf. b) Bestätige deine Vermutung aus Teil a) durch Rechnung.