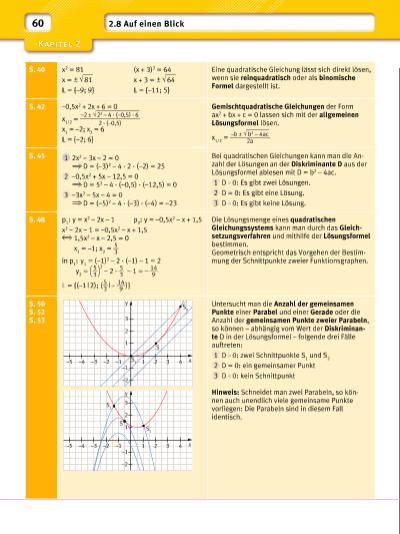
S. 40 x2 = 81 (x + 3)2 = 64 x = +– √ ___ 81 x + 3 = +– √ ___ 64 = {–9; 9} = {–11; 5} Eine quadratische Gleichung lässt sich direkt lösen, wenn sie reinquadratisch oder als binomische Formel dargestellt ist. S. 42 –0,5x2 + 2x + 6 = 0 x 1/2 = –2 ± √ _____________ 22 – 4 · (–0,5) · 6 _________________ 2 · (–0,5) x 1 = –2; x 2 = 6 = {–2; 6} Gemischtquadratische Gleichungen der Form ax2 + bx + c = 0 lassen sich mit der allgemeinen Lösungs formel lösen. x 1/2 = –b ± √ _______ b2 – 4ac ___________2a S. 45 1 2x2 – 3x – 2 = 0 D = (–3)2 – 4 · 2 · (–2) = 25 2 –0,5x2 + 5x – 12,5 = 0 D = 52 – 4 · (–0,5) · (–12,5) = 0 3 –3x2 – 5x – 4 = 0 D = (–5)2 – 4 · (–3) · (–4) = –23 Bei quadratischen Gleichungen kann man die Anzahl der Lösungen an der Diskriminante D aus der Lösungsformel ablesen mit D = b2 – 4ac. 1 D 0: Es gibt zwei Lösungen. 2 D = 0: Es gibt eine Lösung. 3 D 0: Es gibt keine Lösung. S. 48 p 1 : y = x2 – 2x – 1 p 2 : y = –0,5x2 – x + 1,5 x2 – 2x – 1 = –0,5x2 – x + 1,5 1,5x2 – x – 2,5 = 0 x 1 = –1; x 2 = 5 __ 3 in p 1 : y 1 = (–1)2 – 2 · (–1) – 1 = 2 y 2 = ( 5 __ 3 ) 2 – 2 · 5 __ 3 – 1 = – 14 ___ 9 = {(–1 | 2); ( 5 __ 3 | – 14 ___ 9 )} Die Lösungsmenge eines quadratischen Gleichungs systems kann man durch das Gleichsetzungsverfahren und mithilfe der Lösungsformel bestimmen. Geometrisch entspricht das Vorgehen der Bestimmung der Schnittpunkte zweier Funktionsgraphen. S. 50 S. 52 S. 53 Untersucht man die Anzahl der gemeinsamen Punkte einer Parabel und einer Gerade oder die Anzahl der gemeinsamen Punkte zweier Parabeln, so können – abhängig vom Wert der Diskriminante D in der Lösungsformel – folgende drei Fälle auftreten: 1 D 0: zwei Schnittpunkte S 1 und S 2 2 D = 0: ein gemeinsamer Punkt 3 D 0: kein Schnittpunkt Hinweis: Schneidet man zwei Parabeln, so können auch unendlich viele gemeinsame Punkte vorliegen: Die Parabeln sind in diesem Fall identisch. S 1 S S 2 –1 –1 –2 1 1 2 3 y x2 3 4–2–3–4–5 S S 1 S 2 –1 –1 –2 1 1 2 3 y x2 3 4–2–3–4–5 60 2.8 Auf einen Blick