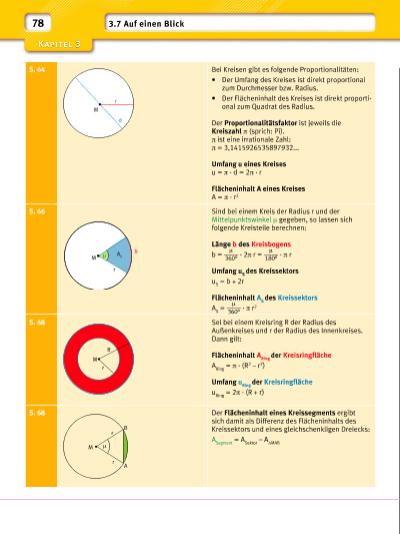
S. 64 Bei Kreisen gibt es folgende Proportionalitäten: • Der Umfang des Kreises ist direkt proportional zum Durchmesser bzw. Radius. • Der Flächeninhalt des Kreises ist direkt proportional zum Quadrat des Radius. Der Proportionalitätsfaktor ist jeweils die Kreiszahl π (sprich: Pi). π ist eine irrationale Zahl: π = 3,1415926535897932... Umfang u eines Kreises u = π · d = 2π · r Flächeninhalt A eines Kreises A = π · r2 S. 66 Sind bei einem Kreis der Radius r und der Mittelpunktswinkel μ gegeben, so lassen sich folgende Kreisteile berechnen: Länge b des Kreisbogens b = μ ____ 360° · 2π r = μ ____ 180° · π r Umfang u S des Kreissektors u S = b + 2r Flächeninhalt A S des Kreissektors A S = μ ____ 360° · π r2 S. 68 Sei bei einem Kreisring R der Radius des Außenkreises und r der Radius des Innenkreises. Dann gilt: Flächeninhalt A Ring der Kreisringfl äche A Ring = π · (R2 – r2) Umfang u Ring der Kreisringfl äche u Ring = 2π · (R + r) S. 68 Der Flächeninhalt eines Kreissegments ergibt sich damit als Differenz des Flächeninhalts des Kreissektors und eines gleichschenkligen Dreiecks: A Segment = A Sektor – AΔMAB M r d M r r μ B A M R r M μ A S r b 78 3.7 Auf einen Blick