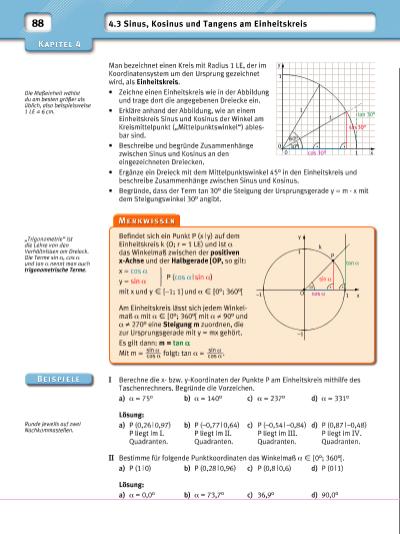
88 4.3 Sinus, Kosinus und Tangens am Einheitskreis cos 30° 30° 60° tan 30° 1 1 1 1 sin 30° y 0 0 x Man bezeichnet einen Kreis mit Radius 1 LE, der im Koordinaten system um den Ursprung gezeichnet wird, als Einheitskreis. • Zeichne einen Einheitskreis wie in der Abbildung und trage dort die angegebenen Dreiecke ein. • Erkläre anhand der Abbildung, wie an einem Einheitskreis Sinus und Kosinus der Winkel am Kreismittelpunkt („Mittelpunktswinkel“) ablesbar sind. • Beschreibe und begründe Zusammenhänge zwischen Sinus und Kosinus an den eingezeichneten Dreiecken. • Ergänze ein Dreieck mit dem Mittelpunktswinkel 45° in den Einheitskreis und beschreibe Zusammenhänge zwischen Sinus und Kosinus. • Begründe, dass der Term tan 30° die Steigung der Ursprungsgerade y = m · x mit dem Steigungswinkel 30° angibt. Die Maßeinheit wählst du am besten größer als üblich, also beispielsweise 1 LE = 6 cm. „Trigonometrie“ ist die Lehre von den Verhältnissen am Dreieck. Die Terme sin α, cos α und tan α nennt man auch trigonometrische Terme. Runde jeweils auf zwei Nachkommastellen. O k P sin α cos α α tan α 1–1 –1 1 y x I Berechne die xbzw. y-Koordinaten der Punkte P am Einheitskreis mithilfe des Taschenrechners. Begründe die Vorzeichen. a) α = 75° b) α = 140° c) α = 237° d) α = 331° Lösung: a) P (0,26 | 0,97) b) P (–0,77 | 0,64) c) P (–0,54 | –0,84) d) P (0,87 | –0,48) P liegt im I. P liegt im II. P liegt im III. P liegt im IV. Quadranten. Quadranten. Quadranten. Quadranten. II Bestimme für folgende Punktkoordinaten das Winkelmaß α X [0°; 360°[. a) P (1 | 0) b) P (0,28 | 0,96) c) P (0,8 | 0,6) d) P (0 | 1) Lösung: a) α = 0,0° b) α = 73,7° c) 36,9° d) 90,0° P (cos α | sin α) Befi ndet sich ein Punkt P (x | y) auf dem Einheitskreis k (O; r = 1 LE) und ist α das Winkelmaß zwischen der positiven x-Achse und der Halbgerade [OP, so gilt: x = cos α y = sin α mit x und y X [–1; 1] und α X [0°; 360°[ Am Einheitskreis lässt sich jedem Winkelmaß α mit α X [0°; 360°[ mit α ≠ 90° und α ≠ 270° eine Steigung m zuordnen, die zur Ursprungsgerade mit y = mx gehört. Es gilt dann: m = tan α Mit m = sin α _____ cos α folgt: tan α = sin α _____ cos α .