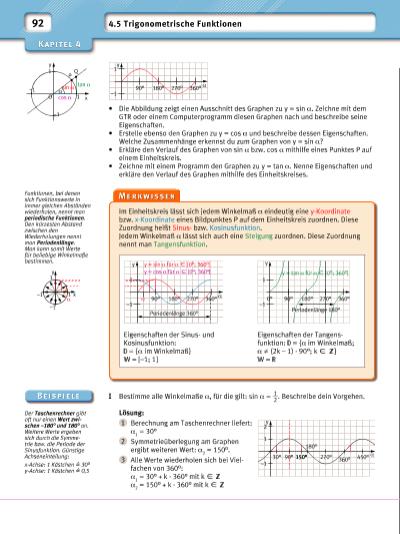
92 4.5 Trigonometrische Funktionen Der Taschen rechner gibt oft nur einen Wert zwischen –180° und 180° an. Weitere Werte ergeben sich durch die Symmetrie bzw. die Periode der Sinusfunktion. Günstige Achseneinteilung: x-Achse: 1 Kästchen = 30° y-Achse: 1 Kästchen = 0,5 Funktionen, bei denen sich Funktionswerte in immer gleichen Abständen wiederholen, nennt man periodische Funktionen. Den kürzesten Abstand zwischen den Wiederholungen nennt man Periodenlänge. Man kann somit Werte für beliebige Winkelmaße bestimmen. • Die Abbildung zeigt einen Ausschnitt des Graphen zu y = sin α. Zeichne mit dem GTR oder einem Computerprogramm diesen Graphen nach und beschreibe seine Eigenschaften. • Erstelle ebenso den Graphen zu y = cos α und beschreibe dessen Eigenschaften. Welche Zusammenhänge erkennst du zum Graphen von y = sin α? • Erkläre den Verlauf des Graphen von sin α bzw. cos α mithilfe eines Punktes P auf einem Einheitskreis. • Zeichne mit einem Programm den Graphen zu y = tan α. Nenne Eigenschaften und erkläre den Verlauf des Graphen mithilfe des Einheitskreises. Im Einheitskreis lässt sich jedem Winkelmaß α eindeutig eine y-Koordinate bzw. x-Koordinate eines Bildpunktes P auf dem Einheitskreis zuordnen. Diese Zuordnung heißt Sinusbzw. Kosinusfunktion. Jedem Winkelmaß α lässt sich auch eine Steigung zuordnen. Diese Zuordnung nennt man Tangensfunktion. I Bestimme alle Winkelmaße α, für die gilt: sin α = 1 __ 2 . Beschreibe dein Vorgehen. Lösung: 1 Berechnung am Taschenrechner liefert: α 1 = 30° 2 Symmetrieüberlegung am Graphen ergibt weiteren Wert: α 2 = 150°. 3 Alle Werte wiederholen sich bei Vielfachen von 360°: α 1 = 30° + k · 360° mit k X α 2 = 150° + k · 360° mit k X 1 y 30° α –1 2 90° 150° 270° 180° 360° 450° Eigenschaften der Sinusund Kosinusfunktion: = {α im Winkelmaß} = [–1; 1] y –1 90° 180° 270° 360° α y = sin α für α X [0°; 360°[ α y = cos α für α X [0°; 360°[ Periodenlänge 360° 1 1 y –1 90°0° 180° 360°270° y = tan α für α X [0°; 360°[ Periodenlänge 180° y x–1 –1 1 1 α Eigenschaften der Tangensfunktion: = {α im Winkelmaß; α ≠ (2k – 1) · 90°; k X } = y –1 90° 180° 270° 360° α 1 –1 –1 P Q 1 x 1 O y sin α cos α α tan α