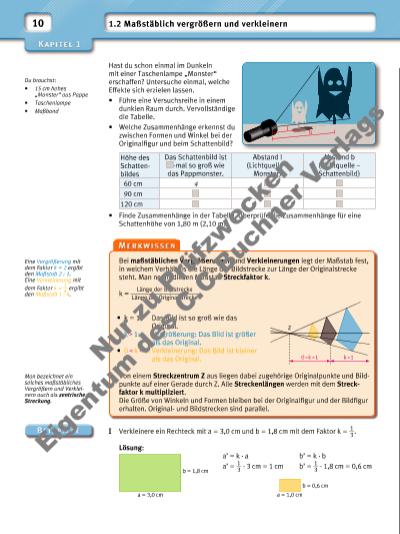
| Volltext anzeigen | |
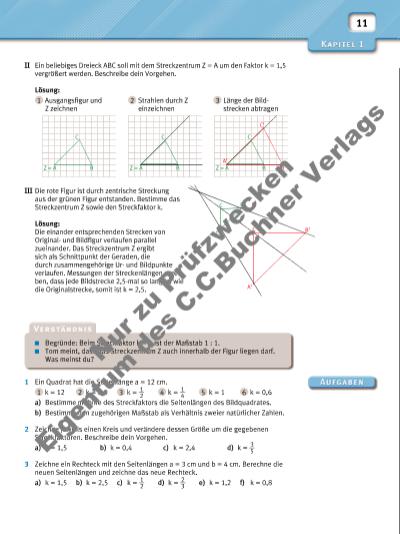
11 II Ein beliebiges Dreieck ABC soll mit dem Streckzentrum Z = A um den Faktor k = 1,5 vergrößert werden. Beschreibe dein Vorgehen. Lösung: 1 Ausgangsfi gur und 2 Strahlen durch Z Z zeichnen einzeichnen III Die rote Figur ist durch zentrische Streckung aus der grünen Figur entstanden. Bestimme das Streckzentrum Z sowie den Streckfaktor k. Lösung: Die einander entsprechenden Strecken von Originalund Bildfi gur verlaufen parallel zueinander. Das Streckzentrum Z ergibt sich als Schnittpunkt der Geraden, die durch zusammengehörige Urund Bildpunkte verlaufen. Messungen der Streckenlängen ergeben, dass jede Bildstrecke 2,5-mal so lang ist wie die Originalstrecke, somit ist k = 2,5. 3 Länge der Bildstrecken abtragen Z = A B C Z = A B C Z = A B B’ C A’ C’ 1 Ein Quadrat hat die Seitenlänge a = 12 cm. 1 k = 12 2 k = 2,5 3 k = 1 __ 2 4 k = 1 __ 4 5 k = 1 6 k = 0,6 a) Bestimme mithilfe des Streckfaktors die Seitenlängen des Bildquadrates. b) Bestimme den zugehörigen Maßstab als Verhältnis zweier natürlicher Zahlen. 2 Zeichne jeweils einen Kreis und verändere dessen Größe um die gegebenen Streckfaktoren. Beschreibe dein Vorgehen. a) k = 1,5 b) k = 0,4 c) k = 2,4 d) k = 3 __ 5 3 Zeichne ein Rechteck mit den Seitenlängen a = 3 cm und b = 4 cm. Berechne die neuen Seitenlängen und zeichne das neue Rechteck. a) k = 1,5 b) k = 2,5 c) k = 1 __ 2 d) k = 2 __ 3 e) k = 1,2 f) k = 0,8 Begründe: Beim Streckfaktor k = 1 ist der Maßstab 1 : 1. Tom meint, dass das Streckzentrum Z auch innerhalb der Figur liegen darf. Was meinst du? A B B’ C A’ C’ Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C .B uc hn er V er la gs | |
 « |  » |
|
» Zur Flash-Version des Livebooks | |