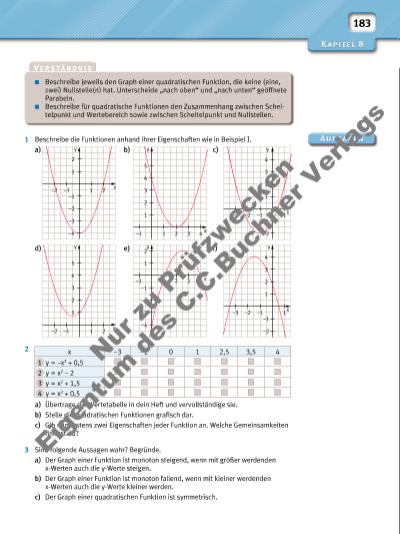
183 21 y x –1 –2 1 2 –2 –1 –3 –4 x 1 2 3 4 –3 –2 –1 1 –1 –2 1 2 y x 1 2 3 4 5 –2 –1 1 2 3 4 y x –1 1 2 –1 –2 –3 –4 y x 1 2 3 4 –3 –2 –1 1 –1 –2 y 2 3 41 y x 1 2 3 4 5 –1 Beschreibe jeweils den Graph einer quadratischen Funktion, die keine (eine, zwei) Nullstelle(n) hat. Unterscheide „nach oben“ und „nach unten“ geöffnete Parabeln. Beschreibe für quadratische Funktionen den Zusammenhang zwischen Scheitelpunkt und Wertebereich sowie zwischen Scheitelpunkt und Nullstellen. 1 Beschreibe die Funktionen anhand ihrer Eigenschaften wie in Beispiel I. a) b) c) d) e) f) 2 a) Übertrage die Wertetabelle in dein Heft und vervollständige sie. b) Stelle die quadratischen Funktionen grafi sch dar. c) Gib mindestens zwei Eigenschaften jeder Funktion an. Welche Gemeinsamkeiten fi ndest du? 3 Sind folgende Aussagen wahr? Begründe. a) Der Graph einer Funktion ist monoton steigend, wenn mit größer werdenden x-Werten auch die y-Werte steigen. b) Der Graph einer Funktion ist monoton fallend, wenn mit kleiner werdenden x-Werten auch die y-Werte kleiner werden. c) Der Graph einer quadratischen Funktion ist symmetrisch. x –3 –2 0 1 2,5 3,5 4 1 y = –x2 + 0,5 2 y = x2 – 2 3 y = x2 + 1,5 4 y = x2 + 0,5 Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C .B uc hn er V er la gs