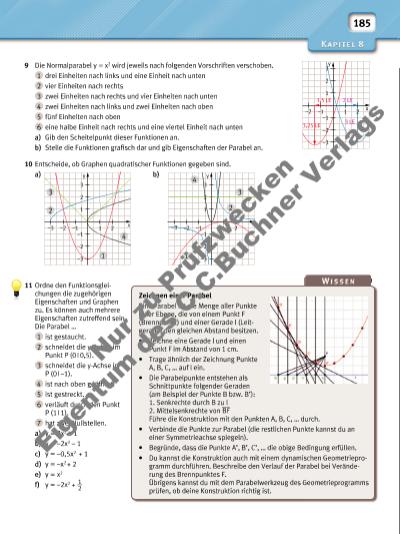
185 9 Die Normalparabel y = x2 wird jeweils nach folgenden Vorschriften verschoben. 1 drei Einheiten nach links und eine Einheit nach unten 2 vier Einheiten nach rechts 3 zwei Einheiten nach rechts und vier Einheiten nach unten 4 zwei Einheiten nach links und zwei Einheiten nach oben 5 fünf Einheiten nach oben 6 eine halbe Einheit nach rechts und eine viertel Einheit nach unten a) Gib den Scheitelpunkt dieser Funktionen an. b) Stelle die Funktionen grafi sch dar und gib Eigenschaften der Parabel an. 10 Entscheide, ob Graphen quadratischer Funktionen gegeben sind. a) b) 11 Ordne den Funktionsgleichungen die zugehörigen Eigenschaften und Graphen zu. Es können auch mehrere Eigenschaften zutreffend sein. Die Parabel … 1 ist gestaucht. 2 schneidet die y-Achse im Punkt P (0 I 0,5). 3 schneidet die y-Achse in P (0 I –1). 4 ist nach oben geöffnet. 5 ist gestreckt. 6 verläuft durch den Punkt P (1 I 1). 7 hat zwei Nullstellen. a) y = 2x2 – 1 b) y = –2x2 – 1 c) y = –0,5x2 + 1 d) y = –x2 + 2 e) y = x2 f) y = –2x2 + 1 __ 2 21 y x –1 –2 1 1 1 2 2 3 –3 –2 –1 –3 21 y –1 –2 1 2 3 –3 –2 –1 –3 3 3 2 4 4 21 y x –1 –2 1 2 3 –2 1,5 LE 2 LE 3 LE 3,25 LE –1 –3 Zeichnen einer Parabel Eine Parabel ist die Menge aller Punkte einer Ebene, die von einem Punkt F (Brennpunkt) und einer Gerade l (Leitgerade) den gleichen Abstand besitzen. • Zeichne eine Gerade l und einen Punkt F im Abstand von 1 cm. • Trage ähnlich der Zeichnung Punkte A, B, C, … auf l ein. • Die Parabelpunkte entstehen als Schnittpunkte folgender Geraden (am Beispiel der Punkte B bzw. B’): 1. Senkrechte durch B zu l 2. Mittelsenkrechte von ___ BF Führe die Konstruktion mit den Punkten A, B, C, … durch. • Verbinde die Punkte zur Parabel (die restlichen Punkte kannst du an einer Symmetrieachse spiegeln). • Begründe, dass die Punkte A’, B’, C’, … die obige Bedingung erfüllen. • Du kannst die Konstruktion auch mit einem dynamischen Geometrieprogramm durchführen. Beschreibe den Verlauf der Parabel bei Veränderung des Brennpunktes F. Übrigens kannst du mit dem Parabelwerkzeug des Geometrieprogramms prüfen, ob deine Konstruktion richtig ist. Nu r z u Pr üf zw ec ke n Ei ge nt um d s C .C .B uc hn er V er la gs