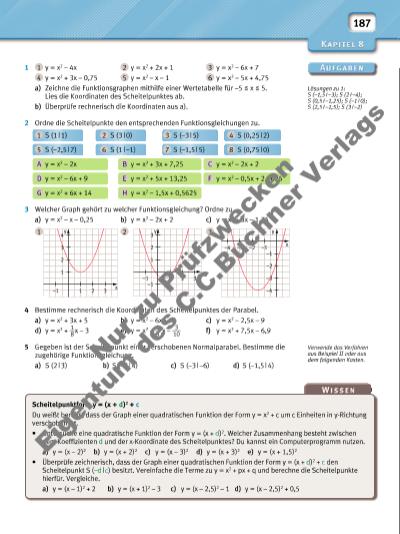
187 1 1 y = x2 – 4x 2 y = x2 + 2x + 1 3 y = x2 – 6x + 7 4 y = x2 + 3x – 0,75 5 y = x2 – x – 1 6 y = x2 – 5x + 4,75 a) Zeichne die Funktionsgraphen mithilfe einer Wertetabelle für –5 x 5. Lies die Koordinaten des Scheitelpunktes ab. b) Überprüfe rechnerisch die Koordinaten aus a). 2 Ordne die Scheitelpunkte den entsprechenden Funktionsgleichungen zu. 1 S (1 | 1) 2 S (3 | 0) 3 S (–3 | 5) 4 S (0,25 | 2) 5 S (–2,5 | 7) 6 S (1 | –1) 7 S (–1,5 | 5) 8 S (0,75 | 0) A y = x2 – 2x B y = x2 + 3x + 7,25 C y = x2 – 2x + 2 D y = x2 – 6x + 9 E y = x2 + 5x + 13,25 F y = x2 – 0,5x + 2,0625 G y = x2 + 6x + 14 H y = x2 – 1,5x + 0,5625 3 Welcher Graph gehört zu welcher Funktionsgleichung? Ordne zu. a) y = x2 – x – 0,25 b) y = x2 – 2x + 2 c) y = x2 + 3x – 1,75 1 2 3 4 Bestimme rechnerisch die Koordinaten des Scheitelpunktes der Parabel. a) y = x2 + 3x + 5 b) y = x2 – 6x + 8 c) y = x2 – 2,5x – 9 d) y = x2 + 1 __ 8 x – 3 e) y = x 2 – 4 __ 5 x – 3 ___ 10 f) y = x 2 + 7,5x – 6,9 5 Gegeben ist der Scheitelpunkt einer verschobenen Normalparabel. Bestimme die zugehörige Funktionsgleichung. a) S (2 | 3) b) S (–2 | 4) c) S (–3 | –6) d) S (–1,5 | 4) Lösungen zu 1: S (–1,5 I –3); S (2 I –4); S (0,5 I –1,25); S (–1 I 0); S (2,5 I –1,5); S (3 I –2) Verwende das Verfahren aus Beispiel II oder aus dem folgenden Kasten. Scheitelpunktform y = (x + d)2 + c Du weißt bereits, dass der Graph einer quadratischen Funktion der Form y = x2 + c um c Einheiten in y-Richtung verschoben ist. • Untersuche eine quadratische Funktion der Form y = (x + d)2. Welcher Zusammenhang besteht zwischen dem Koeffi zienten d und der x-Koordinate des Scheitelpunktes? Du kannst ein Computerprogramm nutzen. a) y = (x – 2)2 b) y = (x + 2)2 c) y = (x – 3)2 d) y = (x + 3)2 e) y = (x + 1,5)2 • Überprüfe zeichnerisch, dass der Graph einer quadratischen Funktion der Form y = (x + d)2 + c den Scheitelpunkt S (–d | c) besitzt. Vereinfache die Terme zu y = x2 + px + q und berechne die Scheitelpunkte hierfür. Vergleiche. a) y = (x – 1)2 + 2 b) y = (x + 1)2 – 3 c) y = (x – 2,5)2 – 1 d) y = (x – 2,5)2 + 0,5 1 2 3 3 y x 1 2 –1 –1 y x–2 –1 –1 –4 –3 –2 –3 –41 2 3 3 y x 4 1 2 –1 N r z u Pr üf zw ec ke n Ei ge nt um d es C .C .B uc hn er V er la gs