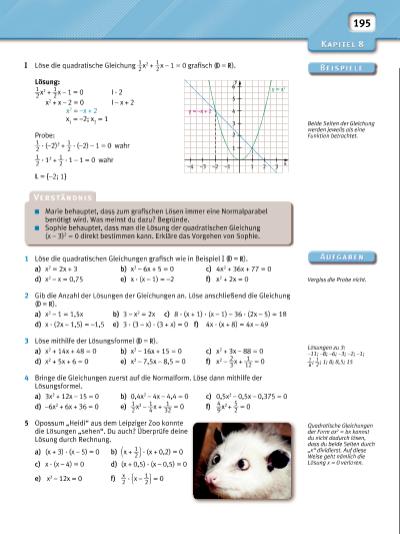
195 Beide Seiten der Gleichung werden jeweils als eine Funktion betrachtet. I Löse die quadratische Gleichung 1 __ 2 x 2 + 1 __ 2 x – 1 = 0 grafi sch ( = ). Lösung: 1 __ 2 x 2 + 1 __ 2 x – 1 = 0 I · 2 x2 + x – 2 = 0 I – x + 2 x2 = –x + 2 x1 = –2; x2 = 1 Probe: 1 __ 2 · (–2) 2 + 1 __ 2 · (–2) – 1 = 0 wahr 1 __ 2 · 1 2 + 1 __ 2 · 1 – 1 = 0 wahr = {–2; 1} 1 Löse die quadratischen Gleichungen grafi sch wie in Beispiel I ( = ). a) x2 = 2x + 3 b) x2 – 6x + 5 = 0 c) 4x2 + 36x + 77 = 0 d) x2 – x = 0,75 e) x · (x – 1) = –2 f) x2 + 2x = 0 2 Gib die Anzahl der Lösungen der Gleichungen an. Löse anschließend die Gleichung ( = ). a) x2 – 1 = 1,5x b) 3 – x2 = 2x c) 8 · (x + 1) · (x – 1) – 36 · (2x – 5) = 18 d) x · (2x – 1,5) = –1,5 e) 3 · (3 – x) · (3 + x) = 0 f) 4x · (x + 8) = 4x – 49 3 Löse mithilfe der Lösungsformel ( = ). a) x2 + 14x + 48 = 0 b) x2 – 16x + 15 = 0 c) x2 + 3x – 88 = 0 d) x2 + 5x + 6 = 0 e) x2 – 7,5x – 8,5 = 0 f) x2 – 2 __ 3 x + 1 ___ 12 = 0 4 Bringe die Gleichungen zuerst auf die Normalform. Löse dann mithilfe der Lösungsformel. a) 3x2 + 12x – 15 = 0 b) 0,4x2 – 4x – 4,4 = 0 c) 0,5x2 – 0,5x – 0,375 = 0 d) –6x2 + 6x + 36 = 0 e) 1 __ 2 x 2 – 1 __ 4 x + 1 ___ 32 = 0 f) 4 __ 9 x 2 + 5 __ 2 = 0 5 Opossum „Heidi“ aus dem Leipziger Zoo konnte die Lösungen „sehen“. Du auch? Überprüfe deine Lösung durch Rechnung. a) (x + 3) · (x – 5) = 0 b) ( x + 1 __ 2 ) · (x + 0,2) = 0 c) x · (x – 4) = 0 d) (x + 0,5) · (x – 0,5) = 0 e) x2 – 12x = 0 f) x __ 2 · ( x – 1 __ 2 ) = 0 Marie behauptet, dass zum grafi schen Lösen immer eine Normalparabel benötigt wird. Was meinst du dazu? Begründe. Sophie behauptet, dass man die Lösung der quadratischen Gleichung (x – 3)2 = 0 direkt bestimmen kann. Erkläre das Vorgehen von Sophie. Vergiss die Probe nicht. Lösungen zu 3: –11; –8; –6; –3; –2; –1; 1 __ 6 ; 1 __ 2 ; 1; 8; 8,5; 15 Quadratische Gleichungen der Form ax2 = bx kannst du nicht dadurch lösen, dass du beide Seiten durch „x“ dividierst. Auf diese Weise geht nämlich die Lösung x = 0 verloren. 1 2 3 3 2 y x 4 5 y = x2 y = –x + 2 6 1 –2 –1–3–4