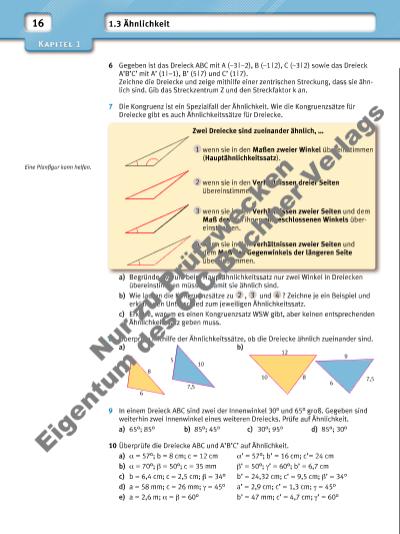
17 11 Überprüfe die Aussage und korrigiere sie gegebenenfalls. Zwei gleichschenklige Dreiecke sind ähnlich, wenn sie in der Größe eines Winkels übereinstimmen. 12 Im Geometrieunterricht werden Geodreiecke zum Zeichnen an der Tafel und im Heft verwendet. Tafeldreieck Großes Geodreieck Kleines Geodreieck a) Überprüfe in deinem Klassenzimmer, in welchen Verhältnis die Seiten der verschiedenen Dreiecke zueinander stehen. Bestimme den Streckfaktor k. b) Bestimme die Dreiecksfl ächen. In welchem Verhältnis stehen sie zueinander? 13 Die Dreiecke ABC und A’B’C’ sind ähnlich zueinander. Berechne die fehlenden Seitenlängen. a) a = 5 cm; b = 7 cm; c = 8,5 cm; a’ = 13,5 cm b) a = 25 mm; b = 45 mm; c = 55 mm; c’ = 11 mm c) b = 45 m; a’ = 38 mm; b’ = 5 cm; c’ = 0,65 dm 14 ΔABC ~ ΔA’B’C’. Berechne die Längen der Strecken x und y. a) b) 15 Konstruiere ein Dreieck ABC mit den gegebenen Maßen. Zeichne anschließend ein zweites Dreieck A’B’C’ so, dass gilt: ΔABC ~ ΔA’B’C. a) a = 6 cm; b = 4,5 cm; γ = 80° a’ = 4 cm b) a = 5 cm; b = 4 cm; c = 7 cm a’ = 3 cm c) b = 5,5 cm; c = 5 cm; α = 80° hb’ = 6 cm 16 Die abgebildete Figur besteht aus Parallelogrammen mit jeweils gleichen Winkeln. a) Begründe, dass die Dreiecke AEK und KFC ähnlich zueinander sind. b) Nenne zwei Dreiecke, die zum Dreieck KCG ähnlich, aber nicht kongruent sind. c) Es gilt: ___ AE = 4 cm; ___ EK = 2,4 cm und __ FC = 1,8 cm. Bestimme die Länge von __ KF. Du kannst das Dreieck A’B’C’ zeichnen, indem du die Seitenlängen a’, b’ und c’ berechnest oder durch Konstruktion grafi sch ermittelst. 7 cm 3 cm 6 cm 6 cm 5 cm 8 cm 12 cm A A A’ A’ B Bx y y C’ B’ C C B’ C’ 4 cm x A B CG KH F E D b a a’ c’ b’ c A B C C’ B’ Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C .B uc hn er V er la gs