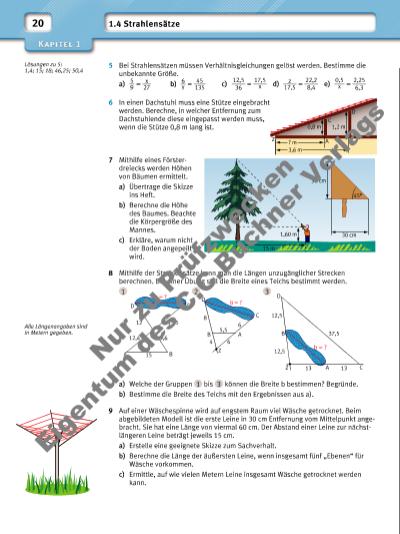
21 10 Der Schatten eines Turms ist 45,5 m lang. Zur gleichen Zeit misst der Schatten eines 1,85 m großen Mannes 2,59 m. Beide Schatten enden im gleichen Punkt. Skizziere die Situation und berechne die Höhe des Turmes. 11 Schon im Altertum wurde, um die Höhe einer Pyramide zu bestimmen, ein Stab senkrecht so aufgestellt, dass die Spitze des Pyramidenschattens auf den Schatten des Stabs fi el. Berechne mithilfe der Werte die Höhe der quadratischen Pyramide. 12 Unbekannte Größen kann man „Pi mal Daumen“ bestimmen. Dazu peilt man einen Gegenstand bei ausgestreckter Armlänge l über den Daumen mit Daumenlänge d an. Bei einem Abstand a lässt sich damit ein Gegenstand der Länge g abdecken. a) Ein Auto ist etwa 4,50 m lang. Bestimme mit deinen Maßen d und l die Entfernung vom Auto. b) Probiere selbst aus, entweder den Abstand a oder die Länge g von Gegenständen mithilfe deiner Daumenlänge und Armlänge zu bestimmen. Umkehrung des 1. Strahlensatzes Werden zwei Geraden a und b, die sich in einem Punkt Z schneiden, von zwei Geraden g und h so geschnitten, dass das Verhältnis der Streckenlängen zugehöriger Abschnitte auf a und b jeweils gleich ist, dann sind die Geraden g und h parallel zueinander. • Begründe rechnerisch, dass die beiden roten Geraden g und h parallel zueinander sind. • Konstruiere mithilfe der Umkehrung des 1. Strahlensatzes zueinander parallele Geraden. • Finde heraus, welche der Geraden m, a, l, e und r in Wirklichkeit parallel zueinander sind. Begründe deine Aussage. Die Zeichnung ist nicht maßstäblich. h 220 m 2 m 6 m 214 m d l g a } 5,2 cm 4,4 cm g h Z a b 5,5 cm 6,5 cm m 4 9 3 2 4 6 Z 6 2 3 5 a l e r Die Zeichnung ist nicht maßstabsgetreu. Nu r z u Pr üf zw ec ke n Ei ge tu m d s C .C .B ch ne r V er la gs