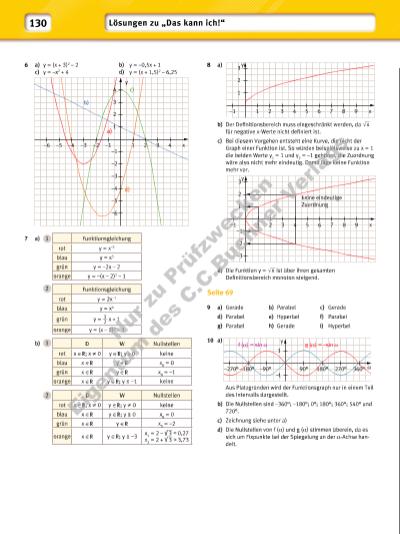
130 Lösungen zu „Das kann ich!“ y –1 –1 1 2 1 2 3 –2 –3 3 keine eindeutige Zuordnung 4 5 6 7 8 9 x 8 a) b) Der Defi nitionsbereich muss eingeschränkt werden, da √ __ x für negative x-Werte nicht defi niert ist. c) Bei diesem Vorgehen entsteht eine Kurve, die nicht der Graph einer Funktion ist. So würden beispielsweise zu x = 1 die beiden Werte y1 = 1 und y2 = –1 gehören, die Zuordnung wäre also nicht mehr eindeutig. Damit läge keine Funktion mehr vor. d) Die Funktion y = √ __ x ist über ihren gesamten Defi nitionsbereich monoton steigend. Seite 69 9 a) Gerade b) Parabel c) Gerade d) Parabel e) Hyperbel f) Parabel g) Parabel h) Gerade i) Hyperbel 10 a) Aus Platzgründen wird der Funktionsgraph nur in einem Teil des Intervalls dargestellt. b) Die Nullstellen sind –360°; –180°; 0°; 180°; 360°; 540° und 720°. c) Zeichnung siehe unter a) d) Die Nullstellen von f (α) und g (α) stimmen überein, da es sich um Fixpunkte bei der Spiegelung an der α-Achse handelt. 6 a) y = (x + 3)2 – 2 b) y = –0,5x + 1 c) y = –x2 + 4 d) y = (x + 1,5)2 – 6,25 7 a) 1 2 b) 1 2 y a) b) d) c) –1 –1 1 2–2–3–4–5–6 1 2 3 4 –2 –3 –4 –5 –6 3 4 x Funktionsgleichung rot y = x–2 blau y = x3 grün y = –2x – 2 orange y = –(x – 2)2 – 1 Nullstellen rot x B ; x ≠ 0 y B ; y 0 keine blau x B y B x0 = 0 grün x B y B x0 = –1 orange x B y B ; y –1 keine Funktionsgleichung rot y = 2x–1 blau y = x4 grün y = 1 __ 2 x + 1 orange y = (x – 2)2 – 3 Nullstellen rot x B ; x ≠ 0 y B ; y ≠ 0 keine blau x B y B ; y 0 x0 = 0 grün x B y B x0 = –2 orange x B y B ; y –3 x1 = 2 – √ __ 3 0,27 x2 = 2 + √ __ 3 3,73 f (α) = sin α g (α) = –sin α –1 90° 1 y α–90°–180°–270° 180° 270° 360° y –1 1 2 1 2 3 3 4 5 6 7 8 9 x Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C .B uc hn er V er la gs