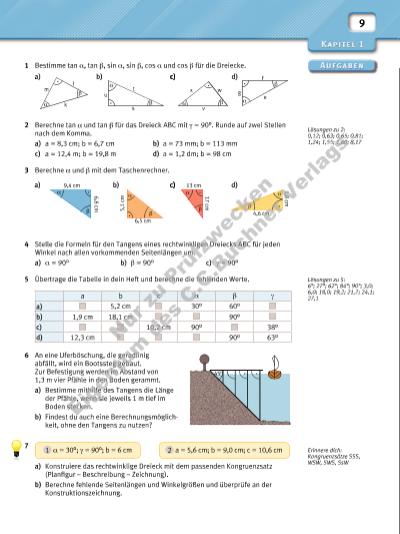
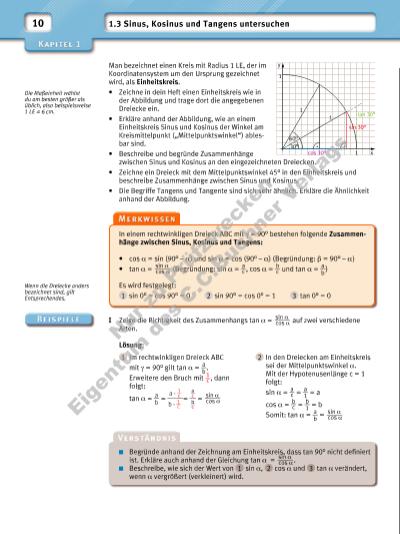
cos 30° 30° 60° tan 30° 1 1 1 1 sin 30° y x 10 Man bezeichnet einen Kreis mit Radius 1 LE, der im Koordinaten system um den Ursprung gezeichnet wird, als Einheitskreis. • Zeichne in dein Heft einen Einheitskreis wie in der Abbildung und trage dort die angegebenen Dreiecke ein. • Erkläre anhand der Abbildung, wie an einem Einheitskreis Sinus und Kosinus der Winkel am Kreismittelpunkt („Mittelpunktswinkel“) ablesbar sind. • Beschreibe und begründe Zusammenhänge zwischen Sinus und Kosinus an den eingezeichneten Dreiecken. • Zeichne ein Dreieck mit dem Mittelpunktswinkel 45° in den Einheitskreis und beschreibe Zusammenhänge zwischen Sinus und Kosinus. • Die Begriffe Tangens und Tangente sind sich sehr ähnlich. Erkläre die Ähnlichkeit anhand der Abbildung. Die Maßeinheit wählst du am besten größer als üblich, also beispielsweise 1 LE = 6 cm. Wenn die Dreiecke anders bezeichnet sind, gilt Entsprechendes. 1.3 Sinus, Kosinus und Tangens untersuchen In einem rechtwinkligen Dreieck ABC mit γ = 90° bestehen folgende Zusammenhänge zwischen Sinus, Kosinus und Tangens: • cos α = sin (90° – α) und sin α = cos (90° – α) (Begründung: β = 90° – α) • tan α = sin α _____ cos α (Begründung: sin α = a __ c , cos α = b __ c und tan α = a __ b ) Es wird festgelegt: 1 sin 0° = cos 90° = 0 2 sin 90° = cos 0° = 1 3 tan 0° = 0 I Zeige die Richtigkeit des Zusammenhangs tan α = sin α _____ cos α auf zwei verschiedene Arten. Lösung: 1 Im rechtwinkligen Dreieck ABC mit γ = 90° gilt tan α = a __ b . Erweitere den Bruch mit 1 __ c , dann folgt: tan α = a __ b = a · 1 __ c _____ b · 1 __ c = a __ c __ b __ c = sin α _____ cos α Begründe anhand der Zeichnung am Einheitskreis, dass tan 90° nicht defi niert ist. Erkläre auch anhand der Gleichung tan α = sin α _____ cos α . Beschreibe, wie sich der Wert von 1 sin α, 2 cos α und 3 tan α verändert, wenn α vergrößert (verkleinert) wird. 2 In den Dreiecken am Einheitskreis sei der Mittelpunktswinkel α. Mit der Hypotenusenlänge c = 1 folgt: sin α = a __ c = a __ 1 = a cos α = b __ c = b __ 1 = b Somit: tan α = a __ b = sin α _____ cos α Nu r z u Pr fzw ec ke n Ei ge nt u d es C .C .B uc hn er V er la gs