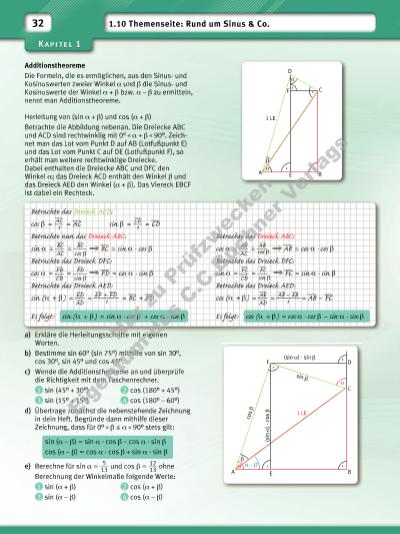
1 LE co s β (s in α ) · c os β F D A E B sin β α (sin α) · sin β α – β β C α α α 1 LE β F C D A E B 1.10 Themenseite: Rund um Sinus & Co.32 Additionstheoreme Die Formeln, die es ermöglichen, aus den Sinusund Kosinuswerten zweier Winkel α und β die Sinusund Kosinuswerte der Winkel α + β bzw. α – β zu ermitteln, nennt man Additionstheoreme. Herleitung von (sin α + β) und cos (α + β) Betrachte die Abbildung nebenan. Die Dreiecke ABC und ACD sind rechtwinklig mit 0° α + β 90°. Zeichnet man das Lot vom Punkt D auf AB (Lotfußpunkt E) und das Lot vom Punkt C auf DE (Lotfußpunkt F), so erhält man weitere rechtwinklige Dreiecke. Dabei enthalten die Dreiecke ABC und DFC den Winkel α; das Dreieck ACD enthält den Winkel β und das Dreieck AED den Winkel (α + β). Das Viereck EBCF ist dabei ein Rechteck. Betrachte das Dreieck ACD: cos β = __ AC __ 1 = __ AC sin β = __ CD __ 1 = __ CD Betrachte nun das Dreieck ABC: sin α = __ BC __ __ AC = __ BC ___ cos β __ BC = sin α · cos β Betrachte das Dreieck DFC: cos α = __ FD __ __ CD = __ FD ___ sin β __ FD = cos α · sin β Betrachte das Dreieck AED: sin (α + β) = __ ED ___ __ AD = __ EF + __ FD ______1 = __ BC + __ FD Es folgt: sin (α + β) = sin α · cos β + cos α · sin β Betrachte das Dreieck ABC: cos α = __ AB __ __ AC = __ AB ___ cos β __ AB = cos α · cos β Betrachte das Dreieck DFC: sin α = __ FC __ __ CD = __ FC ___ sin β __ FC = sin α · sin β Betrachte das Dreieck AED: cos (α + β) = __ AE ___ __ AD = ___ AB – __ EB ______1 = __ AB – __ FC Es folgt: cos (α + β) = cos α · cos β – sin α · sin β a) Erkläre die Herleitungsschritte mit eigenen Worten. b) Bestimme sin 60° (sin 75°) mithilfe von sin 30°, cos 30°, sin 45° und cos 45°. c) Wende die Additionstheoreme an und überprüfe die Richtigkeit mit dem Taschenrechner. 1 sin (45° + 30°) 2 cos (180° + 45°) 3 sin (15° + 15°) 4 cos (180° – 60°) d) Übertrage zunächst die nebenstehende Zeichnung in dein Heft. Begründe dann mithilfe dieser Zeichnung, dass für 0° β α 90° stets gilt: sin (α – β) = sin α · cos β – cos α · sin β cos (α – β) = cos α · cos β + sin α · sin β e) Berechne für sin α = 5 ___ 13 und cos β = 12 ___ 13 ohne Berechnung der Winkelmaße folgende Werte: 1 sin (α + β) 2 cos (α + β) 3 sin (α – β) 4 cos (α – β) Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C .B uc hn er V er la gs