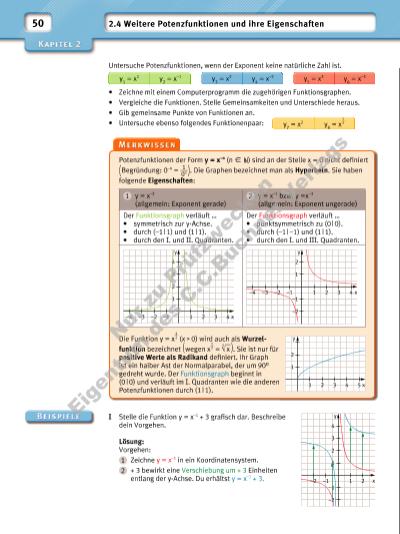
50 2.4 Weitere Potenzfunktionen und ihre Eigenschaften Untersuche Potenzfunktionen, wenn der Exponent keine natürliche Zahl ist. • Zeichne mit einem Computerprogramm die zugehörigen Funktionsgraphen. • Vergleiche die Funktionen. Stelle Gemeinsamkeiten und Unterschiede heraus. • Gib gemeinsame Punkte von Funktionen an. • Untersuche ebenso folgendes Funktionenpaar: y1 = x 1 y3 = x 2 y5 = x 3y2 = x –1 y4 = x –2 y6 = x –3 y7 = x 2 y8 = x 1 __ 2 Potenzfunktionen der Form y = x–n (n X ) sind an der Stelle x = 0 nicht defi niert ( Begründung: 0–n = 1 __ 0n ) . Die Graphen bezeichnet man als Hyperbeln. Sie haben folgende Eigenschaften: Die Funktion y = x 1 __ 2 (x 0) wird auch als Wurzel funktion bezeichnet ( wegen x 1 __ 2 = 2 √ __ x ) . Sie ist nur für positive Werte als Radikand defi niert. Ihr Graph ist ein halber Ast der Normalparabel, der um 90° gedreht wurde. Der Funktionsgraph beginnt in (0 | 0) und verläuft im I. Quadranten wie die anderen Potenz funktionen durch (1 | 1). 1 y = x–2 (allgemein: Exponent gerade) 2 y = x–1 bzw. y =x–3 (allgemein: Exponent ungerade) Der Funktionsgraph verläuft … • symmetrisch zur y-Achse. • durch (–1 | 1) und (1 | 1). • durch den I. und II. Quadranten. Der Funktionsgraph verläuft … • punktsymmetrisch zu (0 | 0). • durch (–1 | –1) und (1 | 1). • durch den I. und III. Quadranten. 1 1 2 3 4 –1–2–3–4 2 3 4 x y 1 1 –1 –2 2 –1–2–3–4 2 3 4 x y 1 1 2 2 3 4 5 x y 1 1 –1 –2 2 3 4 –1–2 2 x yI Stelle die Funktion y = x–1 + 3 grafi sch dar. Beschreibe dein Vorgehen. Lösung: Vorgehen: 1 Zeichne y = x–1 in ein Koordinatensystem. 2 + 3 bewirkt eine Verschiebung um + 3 Einheiten entlang der y-Achse. Du erhältst y = x–1 + 3. Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C .B uc hn er V er la gs