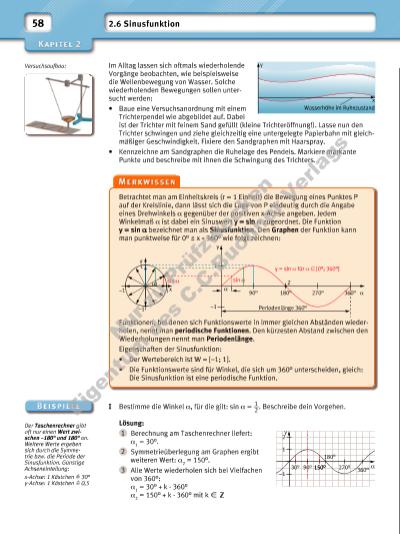
58 2.6 Sinusfunktion Versuchsaufbau: Der Taschen rechner gibt oft nur einen Wert zwischen –180° und 180° an. Weitere Werte ergeben sich durch die Symmetrie bzw. die Periode der Sinusfunktion. Günstige Achseneinteilung: x-Achse: 1 Kästchen = 30° y-Achse: 1 Kästchen = 0,5 Im Alltag lassen sich oftmals wiederholende Vorgänge beobachten, wie beispielsweise die Wellenbewegung von Wasser. Solche wiederholenden Bewegungen sollen untersucht werden: • Baue eine Versuchsanordnung mit einem Trichterpendel wie abgebildet auf. Dabei ist der Trichter mit feinem Sand gefüllt (kleine Trichteröffnung!). Lasse nun den Trichter schwingen und ziehe gleichzeitig eine untergelegte Papierbahn mit gleichmäßiger Geschwindigkeit. Fixiere den Sandgraphen mit Haarspray. • Kennzeichne am Sandgraphen die Ruhelage des Pendels. Markiere markante Punkte und beschreibe mit ihnen die Schwingung des Trichters. Wasserhöhe im Ruhezustand y x Betrachtet man am Einheitskreis (r = 1 Einheit) die Bewegung eines Punktes P auf der Kreislinie, dann lässt sich die Lage von P eindeutig durch die Angabe eines Drehwinkels α gegenüber der positiven x-Achse angeben. Jedem Winkelmaß α ist dabei ein Sinuswert y = sin α zugeordnet. Die Funktion y = sin α bezeichnet man als Sinusfunktion. Den Graphen der Funktion kann man punktweise für 0° x 360° wie folgt zeichnen: Funktionen, bei denen sich Funktionswerte in immer gleichen Abständen wiederholen, nennt man periodische Funktionen. Den kürzesten Abstand zwischen den Wiederholungen nennt man Periodenlänge. Eigenschaften der Sinusfunktion: • Der Wertebereich ist = [–1; 1]. • Die Funktionswerte sind für Winkel, die sich um 360° unterscheiden, gleich: Die Sinusfunktion ist eine periodische Funktion. y P sin α α x–1 –1 1 1 1 y sin α Z –1 90° 180° 270° Periodenlänge 360° 360° α y = sin α für α ∈ [0°; 360°] α I Bestimme die Winkel α, für die gilt: sin α = 1 __ 2 . Beschreibe dein Vorgehen. Lösung: 1 Berechnung am Taschenrechner liefert: α1 = 30°. 2 Symmetrieüberlegung am Graphen ergibt weiteren Wert: α2 = 150°. 3 Alle Werte wiederholen sich bei Vielfachen von 360°: α1 = 30° + k · 360° α2 = 150° + k · 360° mit k X 1 y 30° α –1 2 90° 150° 270° 180° 360° Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C .B uc hn er V er la gs