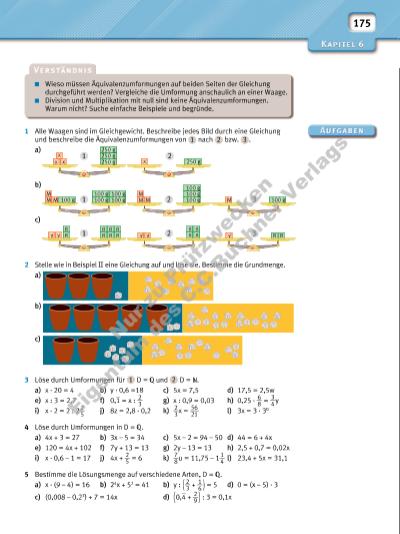
175 Wieso müssen Äquivalenzumformungen auf beiden Seiten der Gleichung durchgeführt werden? Vergleiche die Umformung anschaulich an einer Waage. Division und Multiplikation mit null sind keine Äquivalenzumformungen. Warum nicht? Suche einfache Beispiele und begründe. 1 Alle Waagen sind im Gleichgewicht. Beschreibe jedes Bild durch eine Gleichung und beschreibe die Äquivalenzumformungen von 1 nach 2 bzw. 3 . a) b) c) 2 Stelle wie in Beispiel II eine Gleichung auf und löse sie. Bestimme die Grundmenge. a) b) c) 3 Löse durch Umformungen für 1 D = und 2 D = . a) x · 20 = 4 b) y · 0,6 =18 c) 5x = 7,5 d) 17,5 = 2,5w e) x : 3 = 2,7 f) 0, __ 1 = x : 2 __ 3 g) x : 0,9 = 0,03 h) 0,25 · 6 __ 8 = 3 __ 4 y i) x · 2 = 2 : 2 2 __ 5 j) 8z = 2,8 · 0,2 k) 2 __ 3 x = 56 ___ 21 l) 3x = 3 · 3 0 4 Löse durch Umformungen in D = . a) 4x + 3 = 27 b) 3x – 5 = 34 c) 5x – 2 = 94 – 50 d) 44 = 6 + 4x e) 120 = 4x + 102 f) 7y + 13 = 13 g) 2y – 13 = 13 h) 2,5 + 0,7 = 0,02x i) x · 0,6 – 1 = 17 j) 4x + 2 __ 5 = 6 k) 7 __ 8 u = 11,75 – 1 1 __ 4 l) 23,4 + 5x = 31,1 5 Bestimme die Lösungsmenge auf verschiedene Arten, D = . a) x · (9 – 4) = 16 b) 24x + 52 = 41 b) y : ( 2 __ 3 + 1 __ 6 ) = 5 d) 0 = (x – 5) · 3 c) (0,008 – 0,23) + 7 = 14x d) ( 0, __ 4 + 2 __ 9 ) : 3 = 0,1x y 88y y 8 8 8 8 8 8 8 8 y y 8 8 8 8 100 gM 100 g 100 g 100 g 100 g100 gM M M M M M 100 g 100 g 100 g xx x 250 g 250 g 1 1 1 2 2 x 250 g 2 3 3 250 g Nu r z u Pr üf zw ec ke n Ei ge tu m d es C .C .B uc hn er V er la gs