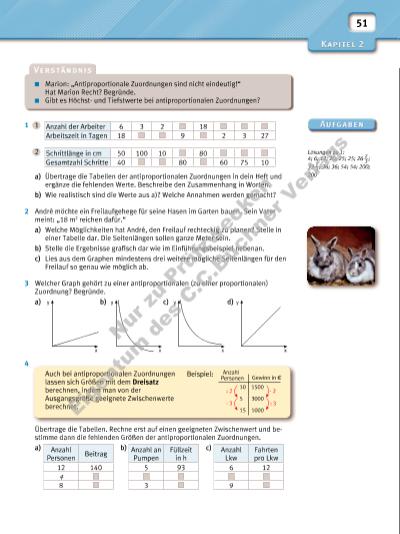
51 Lösungen zu 1: 4; 6; 12; 20; 25; 25; 26 2 __ 3 ; 33 1 __ 3 ; 36; 36; 54; 54; 200; 200 Marion: „Antiproportionale Zuordnungen sind nicht eindeutig!“ Hat Marion Recht? Begründe. Gibt es Höchstund Tiefstwerte bei antiproportionalen Zuordnungen? 1 1 2 a) Übertrage die Tabellen der antiproportionalen Zuordnungen in dein Heft und ergänze die fehlenden Werte. Beschreibe den Zusammenhang in Worten. b) Wie realistisch sind die Werte aus a)? Welche Annahmen werden gemacht? 2 André möchte ein Freilaufgehege für seine Hasen im Garten bauen. Sein Vater meint: „18 m2 reichen dafür.“ a) Welche Möglichkeiten hat André, den Freilauf rechteckig zu planen? Stelle in einer Tabelle dar. Die Seitenlängen sollen ganze Meter sein. b) Stelle die Ergebnisse grafi sch dar wie im Einführungsbeispiel nebenan. c) Lies aus dem Graphen mindestens drei weitere mögliche Seitenlängen für den Freilauf so genau wie möglich ab. 3 Welcher Graph gehört zu einer antiproportionalen (zu einer proportionalen) Zuordnung? Begründe. a) b) c) d) 4 Übertrage die Tabellen. Rechne erst auf einen geeigneten Zwischenwert und bestimme dann die fehlenden Größen der antiproportionalen Zuordnungen. a) b) c) Anzahl der Arbeiter 6 3 2 18 Arbeitszeit in Tagen 18 9 2 3 27 Schrittlänge in cm 50 100 10 80 Gesamtzahl Schritte 40 80 60 75 10 y x y x y x y x Auch bei antiproportionalen Zuordnungen lassen sich Größen mit dem Dreisatz berechnen, indem man von der Ausgangsgröße geeignete Zwischenwerte berechnet. Anzahl Personen Gewinn in f 10 5 15 1500 3000 1000 · 2 : 2 · 3 : 3 Beispiel: Anzahl Personen Beitrag 12 140 4 8 Anzahl an Pumpen Füllzeit in h 5 93 3 Anzahl Lkw Fahrten pro Lkw 6 12 9 Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C .B uc hn er V er la gs