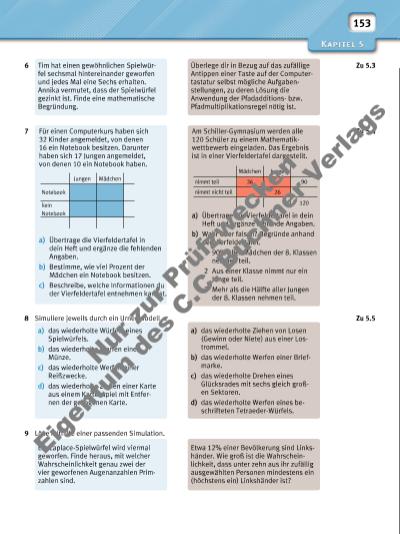
153 a) das wiederholte Würfeln eines Spielwürfels. b) das wiederholte Werfen einer Münze. c) das wiederholte Werfen einer Reißzwecke. d) das wiederholte Ziehen einer Karte aus einem Kartenspiel mit Entfernen der gezogenen Karte. Tim hat einen gewöhnlichen Spielwürfel sechsmal hintereinander geworfen und jedes Mal eine Sechs erhalten. Annika vermutet, dass der Spielwürfel gezinkt ist. Finde eine mathematische Begründung. Ein Laplace-Spielwürfel wird viermal geworfen. Finde heraus, mit welcher Wahrscheinlichkeit genau zwei der vier geworfenen Augenanzahlen Primzahlen sind. a) das wiederholte Ziehen von Losen (Gewinn oder Niete) aus einer Lostrommel. b) das wiederholte Werfen einer Briefmarke. c) das wiederholte Drehen eines Glücksrades mit sechs gleich großen Sektoren. d) das wiederholte Werfen eines beschrifteten Tetraeder-Würfels. Überlege dir in Bezug auf das zufällige Antippen einer Taste auf der Computertastatur selbst mögliche Aufgabenstellungen, zu deren Lösung die Anwendung der Pfadadditionsbzw. Pfadmultiplikationsregel nötig ist. Etwa 12% einer Bevölkerung sind Linkshänder. Wie groß ist die Wahrscheinlichkeit, dass unter zehn aus ihr zufällig ausgewählten Personen mindestens ein (höchstens ein) Linkshänder ist? 8 Simuliere jeweils durch ein Urnenmodell … 6 9 Löse mithilfe einer passenden Simulation. Zu 5.5 Zu 5.3 Am Schiller-Gymnasium werden alle 120 Schüler zu einem Mathematikwettbewerb eingeladen. Das Ergebnis ist in einer Vierfeldertafel dargestellt. a) Übertrage die Vierfeldertafel in dein Heft und ergänze fehlende Angaben. b) Wahr oder falsch? Begründe anhand der Vierfeldertafel. 1 90% aller Mädchen der 8. Klassen nehmen teil. 2 Aus einer Klasse nimmt nur ein Junge teil. 3 Mehr als die Hälfte aller Jungen der 8. Klassen nehmen teil. Für einen Computerkurs haben sich 32 Kinder angemeldet, von denen 16 ein Notebook besitzen. Darunter haben sich 17 Jungen angemeldet, von denen 10 ein Notebook haben. a) Übertrage die Vierfeldertafel in dein Heft und ergänze die fehlenden Angaben. b) Bestimme, wie viel Prozent der Mädchen ein Notebook besitzen. c) Beschreibe, welche Informationen du der Vierfeldertafel entnehmen kannst. Jungen Mädchen Notebook kein Notebook Mädchen Junge nimmt teil nimmt nicht teil 90 120 36 26 Zu 5.47 Nu r z ur P rü fzw ec ke n Ei ge nt um d es C .C . B uc hn er V er la gs