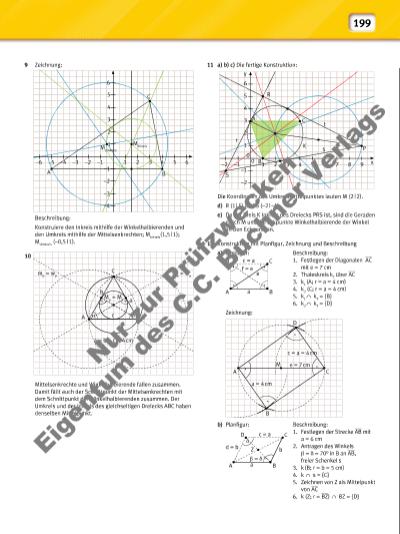
199 6 R C K r s t B S A P y 1 0 0 x 5 4 3 2 1 –1 –2 –1–2 2 3 4 5 6 7 8 9 11 a) b) c) Die fertige Konstruktion: Die Koordinaten des Umkreismittelpunktes lauten M (2 | 2). d) R (1 | 5) und S (–2 | –1) e) Da der Kreis K Inkreis des Dreiecks PRS ist, sind die Geraden durch M und die Eckpunkte Winkelhalbierende der Winkel an den Eckpunkten. 12 Konstruktion mit Planfigur, Zeichnung und Beschreibung a) Planfigur: Beschreibung: 1. Festlegen der Diagonalen ___ AC mit e = 7 cm 2. Thaleskreis kT über ___ AC 3. k1 (A; r = a = 4 cm) 4. k2 (C; r = a = 4 cm) 5. k1T kT = {B} 6. k2T kT = {D} Zeichnung: b) Planfigur: Beschreibung: 1. Festlegen der Strecke ___ AB mit a = 6 cm 2. Antragen des Winkels β = δ = 70° in B an ___ AB, freier Schenkel s 3. k (B; r = b = 5 cm) 4. k T s = {C} 5. Zeichnen von Z als Mittelpunkt von ___ AC 6. k (Z; r = ___ BZ) T BZ = {D} 9 Zeichnung: Beschreibung: Konstruiere den Inkreis mithilfe der Winkelhalbierenden und den Umkreis mithilfe der Mittelsenkrechten; MInkreis(1,5 | 1); MUmkreis (–0,5 | 1). 10 Mittelsenkrechte und Winkelhalbierende fallen zusammen. Damit fällt auch der Schnittpunkt der Mittelsenkrechten mit dem Schnittpunkt der Winkelhalbierenden zusammen. Der Umkreis und der Inkreis des gleichseitigen Dreiecks ABC haben denselben Mittelpunkt. D c = a e f = e aA C B A B D C M e = 7 cm c = a = 4 cm a = 4 cm D δ β = δ d = b a b c = a A C B Z 6 5 4 3 2 1 1 2 3 4 5 6 –1 –1–2–3–4–5–6 A B C M InkreisM Umkreis –2 –3 –4 mb = wβ ma = wα C B Mu = Mi a = b = c = 4 cm A c a b α β Nu r z ur P rü fzw ec ke n Ei ge t m d es C .C . B ch ne r V er la gs