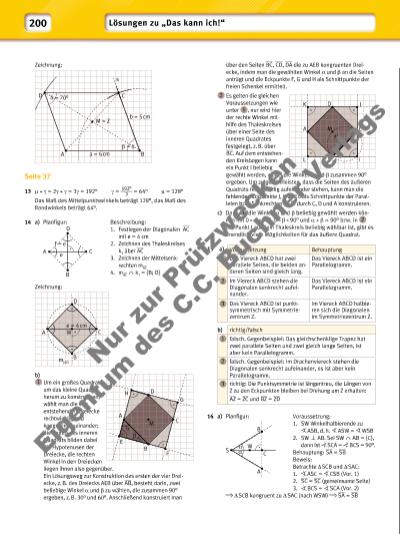
201 b) Planfigur: Voraussetzung: 1. ASW = WSB = α 2. SW AB mit SW T AB = {C} 3. SW ist die Symmetrieachse s. Behauptung: ___ SA = ___ SB Beweis: S s S, W s W, C s C (da S, W, C X s) SA s SB; SB s SA (Vor. 1 und Winkel-/Geradentreue) AB s AB (Vor. 2, Geradentreue) A s A' mit A' X AB und A' X SB B s B' mit B' X AB und B' X SA AB T SB = {B} und AB T SB = {A'} A' = B A s B und B s A s = m __ AB ___ SA = ___ SB 17 Die Aussage ist falsch. In einem Dreieck ist die Summe zweier Seiten immer länger als die dritte Seite (Dreiecksungleichung). 18 Die Aussage ist richtig. 19 Die Aussage ist falsch, z. B. haben folgende Dreiecke zwar die gleiche Gestalt, aber ein Dreieck ist größer als das andere. 20 Die Aussage ist falsch. In jedem Dreieck schneiden sich die Winkelhalbierenden im Mittelpunkt des Inkreises. 21 Die Aussage ist im Allgemeinen Fall falsch. Nur im gleichseitigen Dreieck ist der Mittelpunkt des Umkreises identisch mit dem des Inkreises und damit auch gleich weit von allen Seiten entfernt. 22 Die Aussage ist richtig. Jedes Rechteck lässt sich mittels einer Diagonalen in zwei kongruente rechtwinklige Dreiecke zerlegen. Der Thaleskreis über der gemeinsamen Seite ist für beide Dreiecke auch der Umkreis, also auch für das Rechteck. 23 Die Aussage ist richtig. 24 Die Aussage ist falsch. Sie gilt nur für ein spitzwinkliges Dreieck. Bei einem rechtwinkligen Dreieck liegt der Umkreismittelpunkt auf der Seite des Dreiecks, die dem rechten Winkel gegenüberliegt (Hypotenuse); bei einem stumpfwinkligen Dreieck liegt er außerhalb des Dreiecks. 25 Die Aussage ist falsch, die Umkehrung ist richtig: Der Satz des Thales ist ein Sonderfall des Umfangs winkelsatzes. 26 Die Aussage ist falsch. Ein mathematischer Zusammenhang lässt sich an einem Gegenbeispiel wider legen, für einen Beweis muss man jedoch zeigen, dass der Zusammenhang immer gilt, unabhängig von einem Beispiel. 27 Die Aussage ist falsch: Für den Beweis geometrischer Zusammenhänge verwendet man die Kongruenzsätze für Dreiecke. 28 Die Aussage ist richtig. Lösungen zu „2.11 Das kann ich!“ – Seite 70 1 a) b) Bei jedem Schritt kommen 3 sichtbare Flächen hinzu. Nur beim 1. Schritt hat man 3 + 2 Flächen. Term für die sichtbaren Flächen beim n-ten Schritt: 3 · n + 2 2 a) b) 1 Anzahl der Punkte beim n-ten Schritt: (n + 1) · n 2 Zahl der Punkte beim n-ten Schritt: 3 + 2 · n 3 a) 3x + 8,2y – 4 b) –x2 + 2,5x + 9y c) 2 __ 5 x + 1 1 __ 5 y d) –3x + 4 __ 5 y e) –2x + 2 2 __ 3 y + 14 f) 16,1ab – 6,9b g) 2x2 – 12xy – x + 18y – 3 h) 8x2 + 20x + 8 4 a) 2x + 1 __ 2 x = 2 1 __ 2 x b) 3 1 __ 3 s + 1 – 1 __ 3 s = 1 + 3s c) 2 · ( 1 __ 9 u + 2 __ 7 v ) = 2 __ 9 u + 4 __ 7 v d) (28 + 5t) : (–4) = –7 – 1,25t 5 a) x2 – 2x – 3 b) a2 – 2a – ab + 2b c) –3x2 + 14x – 8 d) 2,5xy + 7x – 2,5y2 – 7y e) 1,44s2 – 1,2st – 0,6s + 0,5t f) –0,9a2 + ab + 5,4a – 6b 6 7 a) x2 – 3x + 2,25 b) 64x2 – 4y2 c) 27 + 18h + 3h2 d) 4x2 + 24x + 36 e) –81y2 + 90xy – 25x2 f) 3 ___ 16 a 2 – 3 ___ 16 ab + 3 ___ 64 b 2 S C B A Wα α SW = s C 33° 88° 58° B A 58° 88° 33° A C B Schritt 1 2 1 2 · 1 = 2 3 + 2 · 1 = 5 2 3 · 2 = 6 3 + 2 · 2 = 7 3 4 · 3 = 12 3 + 2 · 3 = 9 4 5 · 4 = 20 3 + 2 · 4 = 11 5 6 · 5 = 30 3 + 2 · 5 = 13 6 7 · 6 = 42 3 + 2 · 6 = 15 7 8 · 7 = 56 3 + 2 · 7 = 17 8 9 · 8 = 72 3 + 2 · 8 = 19 gemeinsamer Faktor Produktterm a) 7x 7x · (x + 3) b) 6a 6a · (2b – 6a + 3b2) c) 3x2 3x2 · (5x + 4y) d) 0,4kl 0,4kl · (m + 5km – 4) e) 0,2x 0,2x · (4x + 2a – 1) f) –t2 –t2 · (t2 + 1,2 + 4,8ts) Schritt 1 2 3 4 5 6 sichtbare Flächen 5 8 11 14 17 20 Nu r z ur P rü fzw ec ke n E g nt u d es C .C . B uc hn er V er la gs