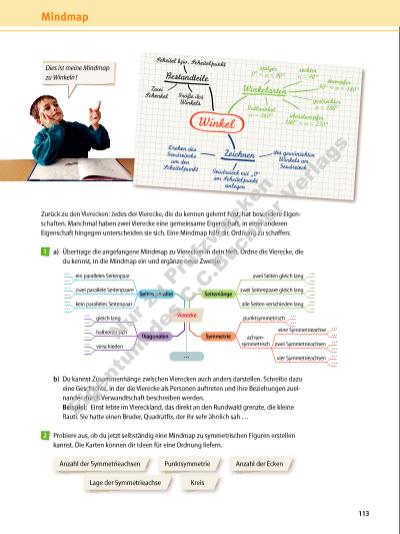
Winkel Bestandteile Zwei Schenkel Größe des Winkels Drehen des Geodreiecks um den Scheitelpunkt Scheitel bzw. Scheitelpunkt Winkelarten Zeichnen Geodreieck mit „0“am Scheitelpunkt anlegen des gewünschten Winkels am Geodreieck spitzer 0° < α < 90° stumpfer 90° < α < 180° überstumpfer 180° < α < 270° Vollwinkel α = 360° gestreckter α = 180° rechter α = 90° Zurück zu den Vierecken: Jedes der Vierecke, die du kennen gelernt hast, hat besondere Eigenschaften. Manchmal haben zwei Vierecke eine gemeinsame Eigenschaft, in einer anderen Eigenschaft hingegen unterscheiden sie sich. Eine Mindmap hilft dir, Ordnung zu schaffen: a) Übertrage die angefangene Mindmap zu Vierecken in dein Heft. Ordne die Vierecke, die du kennst, in die Mindmap ein und ergänze neue Zweige. 1 b) Du kannst Zusammenhänge zwischen Vierecken auch anders darstellen. Schreibe dazu eine Geschichte, in der die Vierecke als Personen auftreten und ihre Beziehungen zueinander durch Verwandtschaft beschreiben werden. Beispiel: Einst lebte im Viereckland, das direkt an den Rundwald grenzte, die kleine Rauti. Sie hatte einen Bruder, Quadratfix, der ihr sehr ähnlich sah … Probiere aus, ob du jetzt selbständig eine Mindmap zu symmetrischen Figuren erstellen kannst. Die Karten können dir Ideen für eine Ordnung liefern. 2 ein paralleles Seitenpaar … … … … … … … … … … … … … … … … … … … … … … … … … … zwei Seiten gleich lang zwei Seitenpaare gleich lang alle Seiten verschieden lang punktsymmetrisch achsensymmetrisch eine Symmetrieachse zwei Symmetrieachsen vier Symmetrieachsen kein paralleles Seitenpaar gleich lang halbieren sich verschieden Diagonalen Seiten parallel Vierecke Seitenlänge … Symmetrie zwei parallele Seitenpaare Dies ist meine Mindmap zu Winkeln ! 113 Mindmap Anzahl der Symmetrieachsen Anzahl der Ecken Lage der Symmetrieachse Kreis Punktsymmetrie Nu r z u Pr üf zw ec ke n Ei g nt um d es C .C .B uc hn er V er la gs