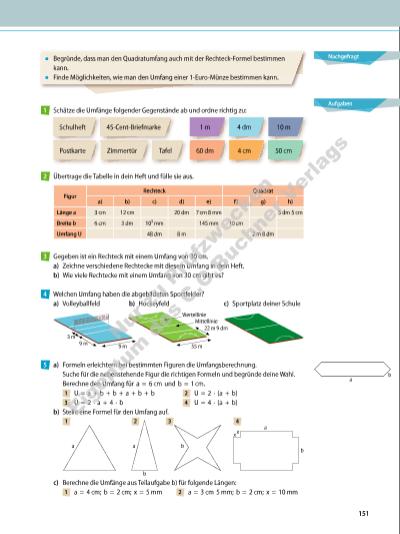
Nachgefragt Aufgaben ▪ Begründe, dass man den Quadratumfang auch mit der Rechteck-Formel bestimmen kann. ▪ Finde Möglichkeiten, wie man den Umfang einer 1-Euro-Münze bestimmen kann. Schätze die Umfänge folgender Gegenstände ab und ordne richtig zu: Übertrage die Tabelle in dein Heft und fülle sie aus. Figur Rechteck Quadrat a) b) c) d) e) f) g) h) Länge a 3 cm 12 cm 20 dm 7 cm 8 mm 5 dm 5 cm Breite b 6 cm 3 dm 10³ mm 145 mm 10 cm Umfang U 48 dm 8 m 2 m 8 dm Gegeben ist ein Rechteck mit einem Umfang von 30 cm. a) Zeichne verschiedene Rechtecke mit diesem Umfang in dein Heft. b) Wie viele Rechtecke mit einem Umfang von 30 cm gibt es? Welchen Umfang haben die abgebildeten Sportfelder? a) Volleyballfeld b) Hockeyfeld c) Sportplatz deiner Schule a) Formeln erleichtern bei bestimmten Figuren die Umfangsberechnung. Suche für die nebenstehende Figur die richtigen Formeln und begründe deine Wahl. Berechne den Umfang für a = 6 cm und b = 1 cm.  U = a + b + b + a + b + b  U = 2 · (a + b)  U = 2 · a + 4 · b  U = 4 · (a + b) b) Stelle eine Formel für den Umfang auf. c) Berechne die Umfänge aus Teilaufgabe b) für folgende Längen:  a = 4 cm; b = 2 cm; x = 5 mm  a = 3 cm 5 mm; b = 2 cm; x = 10 mm 1 Postkarte Zimmertür 45-Cent-Briefmarke Tafel 60 dm 50 cm4 cm 1 m 4 dm 10 mSchulheft 2 3 4 55 m 22 m 9 dm Viertellinie Mittellinie 9 m9 m 3 m 5 a b a b a a xx b b 2 3 41 151 Nu r z u Pr üf zw e ke n Ei ge nt um d es C .C .B uc hn er V er la gs