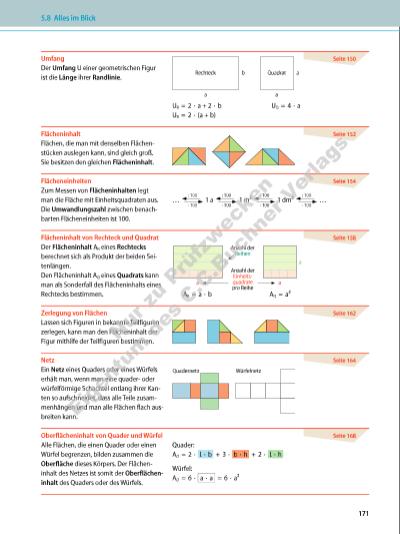
Umfang Der Umfang U einer geometrischen Figur ist die Länge ihrer Randlinie. a a Rechteck Quadratb a UR = 2 · a + 2 · b UQ = 4 · a UR = 2 · (a + b) Seite 150 Flächeninhalt Flächen, die man mit denselben Flächenstücken auslegen kann, sind gleich groß. Sie besitzen den gleichen Flächeninhalt. Seite 152 Flächeneinheiten Zum Messen von Flächeninhalten legt man die Fläche mit Einheitsquadraten aus. Die Umwandlungszahl zwischen benachbarten Flächeneinheiten ist 100. Seite 154 … : 100 · 100 1 a : 100 · 100 1 m² : 100 · 100 1 dm² : 100 · 100 … Flächeninhalt von Rechteck und Quadrat Der Flächeninhalt AR eines Rechtecks berechnet sich als Produkt der beiden Seitenlängen. Den Flächeninhalt AQ eines Quadrats kann man als Sonderfall des Flächeninhalts eines Rechtecks bestimmen. a b a a Anzahl der Reihen Anzahl der Einheitsquadrate pro Reihe AR = a · b AQ = a² Seite 158 Zerlegung von Flächen Lassen sich Figuren in bekannte Teilfiguren zerlegen, kann man den Flächeninhalt der Figur mithilfe der Teilfiguren bestimmen. Seite 162 Netz Ein Netz eines Quaders oder eines Würfels erhält man, wenn man eine quaderoder würfelförmige Schachtel entlang ihrer Kanten so aufschneidet, dass alle Teile zusammenhängen und man alle Flächen flach ausbreiten kann. Quadernetz Würfelnetz Seite 164 Oberflächeninhalt von Quader und Würfel Alle Flächen, die einen Quader oder einen Würfel begrenzen, bilden zusammen die Oberfläche dieses Körpers. Der Flächeninhalt des Netzes ist somit der Oberflächeninhalt des Quaders oder des Würfels. Quader: AO = 2 · l · b + 3 · b · h + 2 · l · h Würfel: AO = 6 · a · a = 6 · a² Seite 168 171 5.8 Alles im Blick Nu r z u Pr üf zw ec ke n Ei ge tu m d es C .C .B uc hn er V er la gs