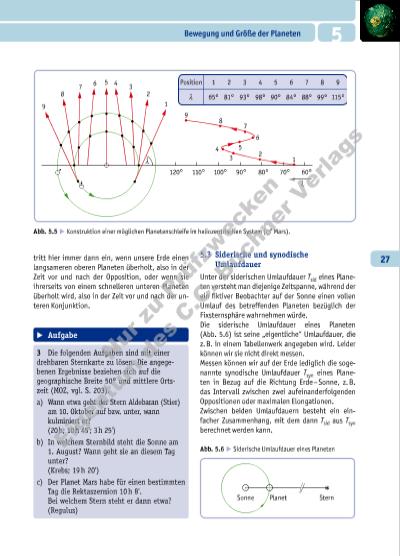
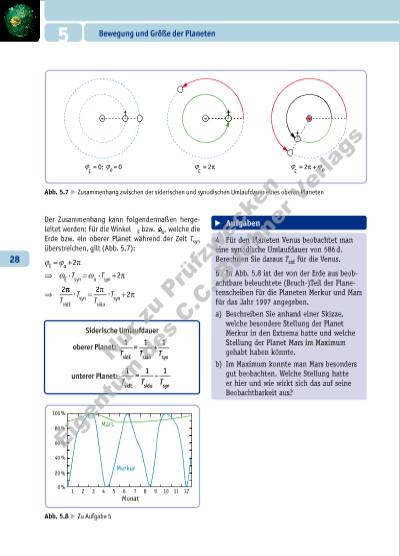
28 5 Bewegung und Größe der Planeten Abb. 5.7 E Zusammenhang zwischen der siderischen und synodischen Umlaufdauer eines oberen Planeten = 2ϕϕ ϕ= 0; E E E = 0 pi pio ϕ = 2 + ϕo Abb. 5.8 E Zu Aufgabe 5 Monat Merkur Mars 1 2 100 % 80 % 60 % 40 % 20 % 0 % 3 4 5 6 7 8 9 10 11 12 E Aufgaben 4 Für den Planeten Venus beobachtet man eine synodische Umlaufdauer von 586 d. Berechnen Sie daraus Tsid für die Venus. 5 In Abb. 5.8 ist der von der Erde aus beobachtbare beleuchtete (Bruch-)Teil der Planetenscheiben für die Planeten Merkur und Mars für das Jahr 1997 angegeben. a) Beschreiben Sie anhand einer Skizze, welche besondere Stellung der Planet Merkur in den Extrema hatte und welche Stellung der Planet Mars im Maximum gehabt haben könnte. b) Im Maximum konnte man Mars besonders gut beobachten. Welche Stellung hatte er hier und wie wirkt sich das auf seine Beobachtbarkeit aus? Der Zusammenhang kann folgendermaßen hergeleitet werden: Für die Winkel ✁E bzw. ✁o, welche die Erde bzw. ein oberer Planet während der Zeit Tsyn überstreichen, gilt (Abb. 5.7): ϕ ϕ ω ω E o E syn o syn = + ⇒ = + ⇒ 2 2 2 pi pi· ·T T pi pi pi T T T T sidE syn sido syn · ·= + 2 2 Siderische Umlaufdauer oberer Planet: 1 = 1 + 1 sidE sido synT T T unterer Planet: 1 = 1 – 1 sidE sidu synT T T N u r zu P rü fz w e c k e E ig e n tu m e s C .C . B u c h n e r V e rl a g s