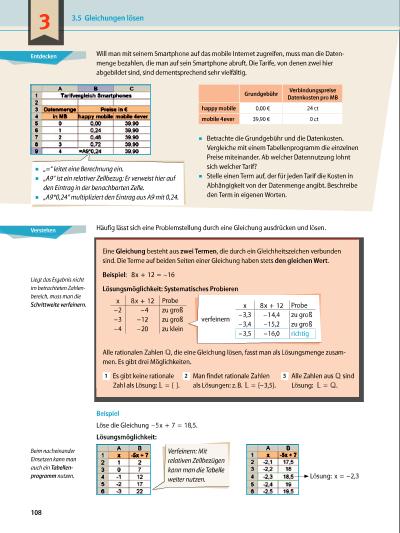
Entdecken Verstehen Eine Gleichung besteht aus zwei Termen, die durch ein Gleichheitszeichen verbunden sind. Die Terme auf beiden Seiten einer Gleichung haben stets den gleichen Wert. Beispiel: 8x + 12 = –16 Lösungsmöglichkeit: Systematisches Probieren x 8x + 12 Probe –2 –4 zu groß –3 –12 zu groß –4 –20 zu klein Alle rationalen Zahlen ℚ, die eine Gleichung lösen, fasst man als Lösungsmenge zusam­ men. Es gibt drei Möglichkeiten. 1 Es gibt keine rationale 2 Man findet rationale Zahlen 3 Alle Zahlen aus ℚ sind Zahl als Lösung: = { }. als Lösungen: z. B. = {–3,5}. Lösung: = ℚ. Liegt das Ergebnis nicht im betrachteten Zahlen­ bereich, muss man die Schrittweite verfeinern. x 8x + 12 Probe –3,3 –14,4 zu groß –3,4 –15,2 zu groß –3,5 –16,0 richtig verfeinern Häufig lässt sich eine Problemstellung durch eine Gleichung ausdrücken und lösen. Beispiel Löse die Gleichung –5x + 7 = 18,5. Lösungsmöglichkeit: Beim nacheinander Einsetzen kann man auch ein Tabellen­ programm nutzen. Verfeinern: Mit relativen Zellbezügen kann man die Tabelle weiter nutzen. Lösung: x = –2,3 Will man mit seinem Smartphone auf das mobile Internet zugreifen, muss man die Daten­ menge bezahlen, die man auf sein Smartphone abruft. Die Tarife, von denen zwei hier abgebildet sind, sind dementsprechend sehr vielfältig. ▪▪ Betrachte die Grundgebühr und die Datenkosten. Vergleiche mit einem Tabellenprogramm die einzelnen Preise mit einander. Ab welcher Datennutzung lohnt sich welcher Tarif? ▪▪ Stelle einen Term auf, der für jeden Tarif die Kosten in Abhängigkeit von der Datenmenge angibt. Beschreibe den Term in eigenen Worten. Grundgebühr Verbindungspreise Datenkosten pro MB happy mobile 0,00 € 24 ct mobile 4ever 39,90 € 0 ct ▪▪ „=“ leitet eine Berechnung ein. ▪▪ „A9“ ist ein relativer Zellbezug: Er verweist hier auf den Eintrag in der benachbarten Zelle. ▪▪ „A9*0,24“ multipliziert den Eintrag aus A9 mit 0,24. 3.5 Gleichungen lösen 108 3