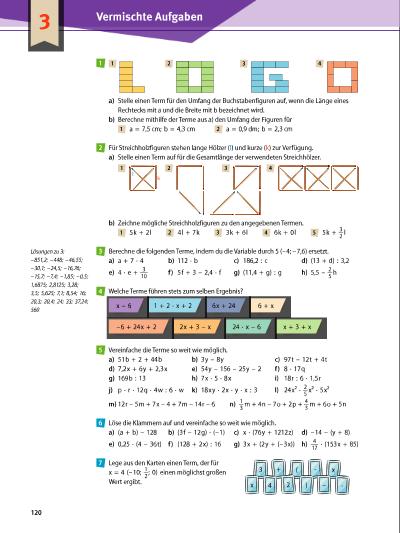
a) Stelle einen Term für den Umfang der Buchstabenfiguren auf, wenn die Länge eines Rechtecks mit a und die Breite mit b bezeichnet wird. b) Berechne mithilfe der Terme aus a) den Umfang der Figuren für 1 a = 7,5 cm; b = 4,3 cm 2 a = 0,9 dm; b = 2,3 cm Für Streichholzfiguren stehen lange Hölzer (l) und kurze (k) zur Verfügung. a) Stelle einen Term auf für die Gesamtlänge der verwendeten Streichhölzer. b) Zeichne mögliche Streichholzfiguren zu den angegebenen Termen. 1 5k + 2l 2 4l + 7k 3 3k + 6l 4 6k + 0l 5 5k + 3 __ 2 l Berechne die folgenden Terme, indem du die Variable durch 5 (–4; –7,6) ersetzt. a) a + 7 ∙ 4 b) 112 ∙ b c) 186,2 : c d) (13 + d) : 3,2 e) 4 ∙ e + 3 ___ 10 f) 5f + 3 – 2,4 ∙ f g) (11,4 + g) : g h) 5,5 – 2 __ 5 h Welche Terme führen stets zum selben Ergebnis? Vereinfache die Terme so weit wie möglich. a) 51b + 2 + 44b b) 3y – 8y c) 97t – 12t + 4t d) 7,2x + 6y + 2,3x e) 54y – 156 – 25y – 2 f) 8 ∙ 17q g) 169b : 13 h) 7x ∙ 5 ∙ 8x i) 18r : 6 ∙ 1,5r j) p ∙ r ∙ 12q ∙ 4w : 6 ∙ w k) 18xy ∙ 2x ∙ y ∙ x : 3 l) 24x2 ∙ 2 __ 5 x2 ∙ 5x2 m) 12r – 5m + 7x – 4 + 7m – 14r – 6 n) 1 __ 3 m + 4n – 7o + 2p + 4 __ 3 m + 6o + 5n Löse die Klammern auf und vereinfache so weit wie möglich. a) (a + b) – 128 b) (3f – 12g) ∙ (–1) c) x ∙ (76y + 1212z) d) –14 – (y + 8) e) 0,25 ∙ (4 – 36t) f) (128 + 2x) : 16 g) 3x + (2y + (–3x)) h) 4 ___ 17 · (153x + 85) Lege aus den Karten einen Term, der für x = 4 (–10; 1 __ 2 ; 0) einen möglichst großen Wert ergibt. 1 1 2 3 4 2 l k 1 2 3 4 3Lösungen zu 3: –851,2; –448; –46,55; –30,1; –24,5; –16,76; –15,7; –7,4; –1,85; –0,5; 1,6875; 2,8125; 3,28; 3,5; 5,625; 7,1; 8,54; 16; 20,3; 20,4; 24; 33; 37,24; 560 4 –6 + 24x + 2 24 · x – 6 x + 3 + x2x + 3 – x x – 6 6 + x1 + 2 · x + 2 6x + 24 5 6 7 3 + ( · x x 4 2 – ·) 3 Vermischte Aufgaben 120