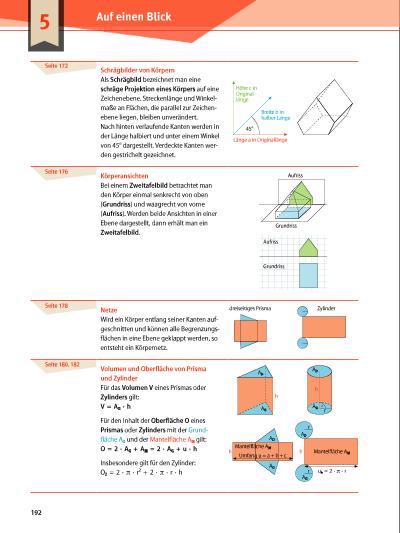
Seite 172 Schrägbilder von Körpern Als Schrägbild bezeichnet man eine schräge Projektion eines Körpers auf eine Zeichenebene. Streckenlänge und Winkel­ maße an Flächen, die parallel zur Zeichen­ ebene liegen, bleiben unverändert. Nach hinten verlaufende Kanten werden in  der Länge halbiert und unter einem Winkel von 45° dargestellt. Verdeckte Kanten wer­ den gestrichelt gezeichnet. Schrägbild eines Quaders 45° Breite b in halber Länge Länge a in Originallänge Höhe c in Originallänge Seite 176 Körperansichten Bei einem Zweitafelbild betrachtet man den Körper einmal senkrecht von oben (Grundriss) und waagrecht von vorne (Aufriss). Werden beide Ansichten in einer Ebene dargestellt, dann erhält man ein Zweitafelbild. Aufriss Grundriss Aufriss Grundriss Seite 178 Netze Wird ein Körper entlang seiner Kanten auf­ geschnitten und können alle Begrenzungs­ flächen in eine Ebene geklappt werden, so entsteht ein Körpernetz. Seite 180, 182 Volumen und Oberfläche von Prisma und Zylinder Für das Volumen V eines Prismas oder Zylinders gilt: V = AG ∙ h Für den Inhalt der Oberfläche O eines Prismas oder Zylinders mit der Grund­ fläche AG und der Mantelfläche AM gilt: O = 2 ∙ AG + AM = 2 ∙ AG + u · h Insbesondere gilt für den Zylinder: OZ = 2 ∙ π ∙ r2 + 2 ∙ π ∙ r ∙ h r r uA = 2 · pi · r Mantelfläche AMh AG AG AD Mantelfläche AM h AD h AG AD r h AG AD Umfang u = a + b + c dreiseitiges Prisma Zylinder 5 Auf einen Blick 192