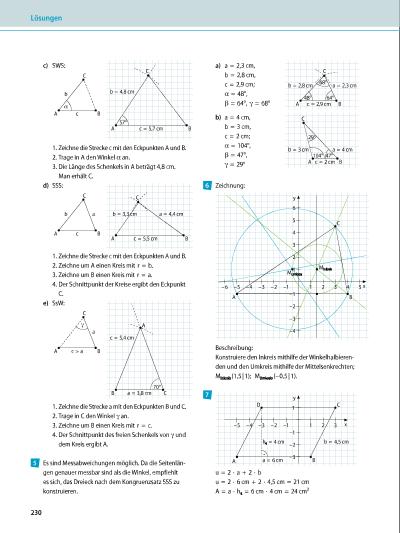
230 c) SWS: 1. Zeichne die Strecke c mit den Eckpunkten A und B. 2. Trage in A den Winkel α an. 3. Die Länge des Schenkels in A beträgt 4,8 cm. Man erhält C. d) SSS: 1. Zeichne die Strecke c mit den Eckpunkten A und B. 2. Zeichne um A einen Kreis mit r = b. 3. Zeichne um B einen Kreis mit r = a. 4. Der Schnittpunkt der Kreise ergibt den Eckpunkt C. e) SsW: 1. Zeichne die Strecke a mit den Eckpunkten B und C. 2. Trage in C den Winkel γ an. 3. Zeichne um B einen Kreis mit r = c. 4. Der Schnittpunkt des freien Schenkels von γ und dem Kreis ergibt A. Es sind Messabweichungen möglich. Da die Seitenlän­ gen genauer messbar sind als die Winkel, empfiehlt es sich, das Dreieck nach dem Kongruenzsatz SSS zu konstruieren. A B C c = 5,7 cm b = 4,8 cm 57° C BA c α b A B C c = 5,5 cm b = 3,3 cm a = 4,4 cm C BA c b a B 70° C A a = 3,8 cm c = 5,4 cm C BA c > a a γ 5 a) a = 2,3 cm, b = 2,8 cm, c = 2,9 cm; α = 48°, β = 64°, γ = 68° b) a = 4 cm, b = 3 cm, c = 2 cm; α = 104°, β = 47°, γ = 29° Zeichnung: Beschreibung: Konstruiere den Inkreis mithilfe der Winkelhalbieren­ den und den Umkreis mithilfe der Mittelsenkrechten; MInkreis (1,5 | 1); MUmkreis (–0,5 | 1). u = 2 · a + 2 · b u = 2 · 6 cm + 2 · 4,5 cm = 21 cm A = a · ha = 6 cm · 4 cm = 24 cm2 c = 2,9 cm b = 2,8 cm a = 2,3 cm C BA 64°48° 68° c = 2 cm b = 3 cm a = 4 cm C BA 47°104° 29° 6 x–6 –5 –4 –3 –2 –1 1 2 3 4 5 y 2 1 –1 –2 –3 –4 3 4 5 6 MInkreis MUmkreis A B C 7 ha = 4 cm A B D C b = 4,5 cm a = 6 cm x–5 –4 –3 –2 –1 1 2 3 y –3 –2 –1 1 Lösungen