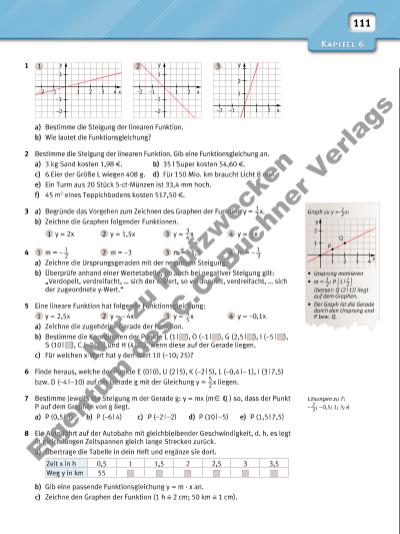
111 1 a) Bestimme die Steigung der linearen Funktion. b) Wie lautet die Funktionsgleichung? 2 Bestimme die Steigung der linearen Funktion. Gib eine Funktionsgleichung an. a) 3 kg Sand kosten 1,98 f. b) 35 l Super kosten 54,60 f. c) 6 Eier der Größe L wiegen 408 g. d) Für 150 Mio. km braucht Licht 8 min. e) Ein Turm aus 20 Stück 5-ct-Münzen ist 33,4 mm hoch. f) 45 m2 eines Teppichbodens kosten 517,50 f. 3 a) Begründe das Vorgehen zum Zeichnen des Graphen der Funktion y = 1 __ 2 x. b) Zeichne die Graphen folgender Funktionen. 1 y = 2x 2 y = 1,5x 3 y = 3 __ 4 x 4 y = 1 __ 5 x 4 1 m = – 1 __ 2 2 m = –3 3 m = –1,5 4 m = – 1 __ 3 a) Zeichne die Ursprungsgeraden mit der negativen Steigung. b) Überprüfe anhand einer Wertetabelle, ob auch bei negativer Steigung gilt: „Verdopelt, verdreifacht, … sich der x-Wert, so verdoppelt, verdreifacht, … sich der zugeordnete y-Wert.“ 5 Eine lineare Funktion hat folgende Funktionsgleichung: 1 y = 2,5x 2 y = – 4x 3 y = 4 __ 5 x 4 y = –0,1x a) Zeichne die zugehörige Gerade der Funktion. b) Bestimme die Koordinaten der Punkte L (1 | ), O (–1 | ), G (2,5 | ), I (–5 | ), S (10 | ), C (–2 | ) und H (4 | ), wenn diese auf der Gerade liegen. c) Für welchen x-Wert hat y den Wert 10 (–10; 25)? 6 Finde heraus, welche der Punkte E (0 | 0), U (2 | 5), K (–2 | 5), L (–0,4 | – 1), I (3 | 7,5) bzw. D (–4 | –10) auf der Gerade g mit der Gleichung y = 5 __ 2 x liegen. 7 Bestimme jeweils die Steigung m der Gerade g: y = mx (mX ) so, dass der Punkt P auf dem Graphen von g liegt. a) P (0,5 | 3) b) P (–6 | 4) c) P (–2 | –2) d) P (10 | –5) e) P (1,5 | 7,5) 8 Ein Auto fährt auf der Autobahn mit gleichbleibender Geschwindigkeit, d. h. es legt in gleich langen Zeitspannen gleich lange Strecken zurück. a) Übertrage die Tabelle in dein Heft und ergänze sie dort. b) Gib eine passende Funktionsgleichung y = m · x an. c) Zeichne den Graphen der Funktion (1 h 2 cm; 50 km 1 cm). Lösungen zu 7: – 2 __ 3 ; – 0,5; 1; 5; 6 Graph zu y = 1 __ 2 x: • Ursprung markieren • m = 1 __ 2 : P ( 1 | 1 __ 2 ) (besser: Q (2 | 1)) liegt auf dem Graphen. • Der Graph ist die Gerade durch den Ursprung und P bzw. Q. Zeit x in h 0,5 1 1,5 2 2,5 3 3,5 Weg y in km 55 1 1–1 2 3 4–2 x –1 –2 y 1 1–1 2–2 x –1 –2 y 1 1–1 2–2 x 2 y1 2 3 y P Q x4321 1 2 N r z P rü fzw ec ke n Ei ge nt um d es C .C . B uc hn er V er la gs