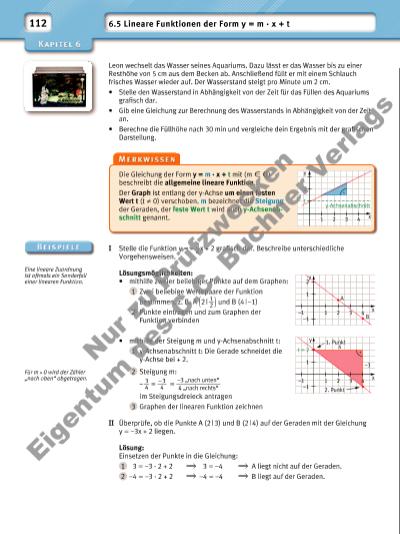
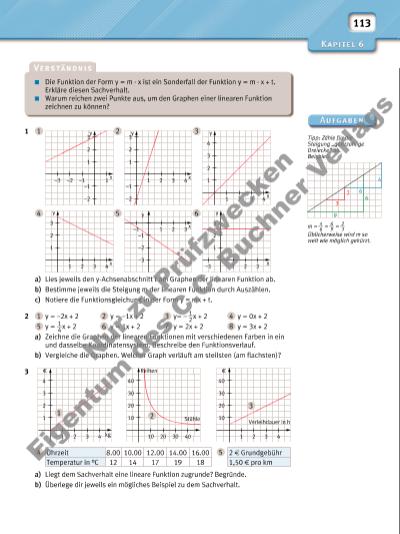
113 Tipp: Zähle für die Steigung „ganzzahlige Dreiecke“ ab. Beispiel: m = 4 __ 6 = 6 __ 9 = 2 __ 3 Üblicherweise wird m so weit wie möglich gekürzt. 1 1 2 3 4 5 6 a) Lies jeweils den y-Achsenabschnitt t am Graphen der linearen Funktion ab. b) Bestimme jeweils die Steigung m der linearen Funktion durch Auszählen. c) Notiere die Funktionsgleichung in der Form y = mx + t. 2 1 y = –2x + 2 2 y = –1x + 2 3 y= – 1 __ 2 x + 2 4 y = 0x + 2 5 y = 1 __ 4 x + 2 6 y = 1x + 2 7 y = 2x + 2 8 y = 3x + 2 a) Zeichne die Graphen der linearen Funktionen mit verschiedenen Farben in ein und dasselbe Koordinatensystem. Beschreibe den Funktionsverlauf. b) Vergleiche die Graphen. Welcher Graph verläuft am steilsten (am fl achsten)? 3 4 5 a) Liegt dem Sachverhalt eine lineare Funktion zugrunde? Begründe. b) Überlege dir jeweils ein mögliches Beispiel zu dem Sachverhalt. Die Funktion der Form y = m · x ist ein Sonderfall der Funktion y = m · x + t. Erkläre diesen Sachverhalt. Warum reichen zwei Punkte aus, um den Graphen einer linearen Funktion zeichnen zu können? 1 3 y x 1 2 –1–2–3 –1 –2 4 3 y x 1 2 321 –1 –2 3 y x –2 –3 –1 21–1 4 3 y x 4 1 2 321 3 y x 1 2 321–14 3 y x 1 2 321 4 9 6 3 2 6 4 3 4 1 2 321 kg 40 30 40 10 20 302010 4 30 40 10 20 321 Reihen Stühle Verleihdauer in h f f Uhrzeit 8.00 10.00 12.00 14.00 16.00 Temperatur in °C 12 14 17 19 18 2 f Grundgebühr 1,50 f pro km 1 2 3 Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C . B uc hn er V er ag s