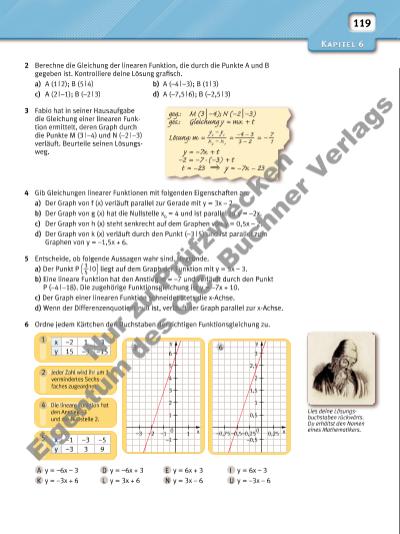
119 2 Berechne die Gleichung der linearen Funktion, die durch die Punkte A und B gegeben ist. Kontrolliere deine Lösung grafi sch. a) A (1 | 2); B (5 | 4) b) A (–4 | –3); B (1 | 3) c) A (2 | –1); B (–2 | 3) d) A (–7,5 | 6); B (–2,5 | 3) 3 Fabio hat in seiner Hausaufgabe die Gleichung einer linearen Funktion ermittelt, deren Graph durch die Punkte M (3 | –4) und N (–2 | –3) verläuft. Beurteile seinen Lösungsweg. 4 Gib Gleichungen linearer Funktionen mit folgenden Eigenschaften an. a) Der Graph von f (x) verläuft parallel zur Gerade mit y = 3x – 2. b) Der Graph von g (x) hat die Nullstelle x0 = 4 und ist parallel zu y = –2x. c) Der Graph von h (x) steht senkrecht auf dem Graphen von y = 0,5x – 2. d) Der Graph von k (x) verläuft durch den Punkt (–3 | 5) und ist parallel zum Graphen von y = –1,5x + 6. 5 Entscheide, ob folgende Aussagen wahr sind. Begründe. a) Der Punkt P ( 3 __ 5 | 0 ) liegt auf dem Graph der Funktion mit y = 5x – 3. b) Eine lineare Funktion hat den Anstieg m = –7 und verläuft durch den Punkt P (–4 | –18). Die zugehörige Funktionsgleichung ist y = –7x + 10. c) Der Graph einer linearen Funktion schneidet stets die x-Achse. d) Wenn der Differenzenquotient null ist, verläuft der Graph parallel zur x-Achse. 6 Ordne jedem Kärtchen den Buchstaben der richtigen Funktionsgleichung zu. A y = –6x – 3 D y = –6x + 3 E y = 6x + 3 I y = 6x – 3 K y = –3x + 6 L y = 3x + 6 N y = 3x – 6 U y = –3x – 6 geg.: M (3 | –4); N (–2 | –3) ges.: Gleichung y = mx + t Lösung: m = y2 – y1 _____ x2 – x1 = –4 – 3 _____3 – 2 = – 7 __ 1 y = –7x + t –2 = –7 · (–3) + t t = –23 y = –7x – 23 y 10 1 –1 2 3 –3 –2 –1 4 x 5 6 Die lineare Funktion hat den Anstieg –3 und die Nullstelle 2. 4 5 y 0,250 0,5 –0,5 1 1,5 2 x 2,5 3 –0,25–0,5–0,75 6 1 Jeder Zahl wird ihr um 3 vermindertes Sechsfaches zugeordnet. 2 3 x –2 1 3 y 15 –3 –15 x –1 –3 –5 y –3 3 9 Lies deine Lösungsbuchstaben rückwärts. Du erhältst den Namen eines Mathematikers. Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C . B uc hn er V er la gs