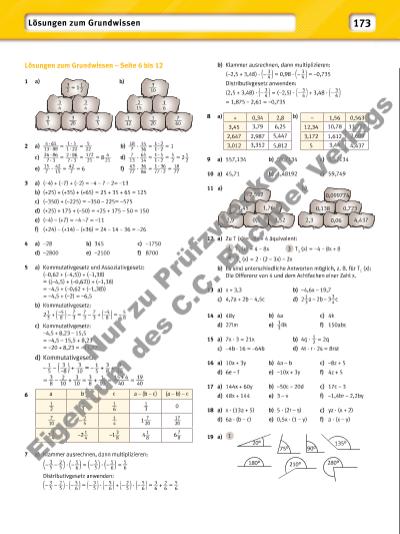
173 b) Klammer ausrechnen, dann multiplizieren: (–2,5 + 3,48) · ( – 3 __ 4 ) = 0,98 · ( – 3 __ 4 ) = –0,735 Distributivgesetz anwenden: (2,5 + 3,48) · ( – 3 __ 4 ) = (–2,5) · ( – 3 __ 4 ) + 3,48 · ( – 3 __ 4 ) = 1,875 – 2,61 = –0,735 8 a) b) 9 a) 557,134 b) 55,7134 c) 5,57134 10 a) 45,71 b) 1,48192 c) 59,749 11 12 a) Zu T (x) = –8x + 4 äquivalent: 1 T1 (x) = 4 – 8x 3 T3 (x) = –4 – 8x + 8 4 T4 (x) = 2 · (2 – 3x) – 2x b) Es sind unterschiedliche Antworten möglich, z. B. für T1 (x): Die Differenz von 4 und dem Achtfachen einer Zahl x. 13 a) x + 3,3 b) –4,6x – 19,7 c) 4,7a + 2b – 4,5c d) 2 1 __ 3 a – 2b – 3 3 __ 4 c 14 a) 48y b) 4a c) 4k d) 27lm e) 1 __ 3 ilk f) 150abc 15 a) 7x · 3 = 21x b) 4q · 1 __ 2 = 2q c) –4b · 16 = –64b d) 4t · r · 2s = 8rst 16 a) 10x + 3y b) 4a – b c) –8z + 5 d) 6e – f e) –10x + 3y f) 4z + 5 17 a) 144x + 60y b) –50c – 20d c) 17c – 3 d) 48x + 144 e) 3 – v f) –1,4br – 2,2by 18 a) x · (13a + 5) b) 5 · (2r – s) c) yz · (x + 2) d) 6a · (b – c) e) 0,5x · (1 – y) f) a · (x – y) 19 a) 1 Lösungen zum Grundwissen Lösungen zum Grundwissen – Seite 6 bis 12 1 2 a) 4 · 65 ______ 13 · 88 = 1 · 5 _____ 1 · 22 = 5 ___ 22 b) 18 ___ 7 · 14 ___ 36 = 1 · 2 ____1 · 2 = 1 c) 24 · 86 ______7 · 3 = 2 · 86 _____7 · 3 = 172 ____ 21 = 8 4 ___ 21 d) 7 ___ 13 · 65 ___ 14 = 1 · 5 ____1 · 2 = 5 __ 2 = 2 1 __ 2 e) 15 ___ 7 · 42 ___ 15 = 42 ___ 7 = 6 f) 43 ___ 77 · 36 ___ 86 = 1 · 36 _____77 · 2 = 18 ___ 77 3 a) (–4) + (–7) + (–2) = –4 – 7 – 2= –13 b) (+25) + (+35) + (+65) = 25 + 35 + 65 = 125 c) (–350) + (–225) = –350 – 225= –575 d) (+25) + 175 + (–50) = +25 + 175 – 50 = 150 e) (–4) – (+7) = –4 –7 = –11 f) (+24) – (+14) – (+36) = 24 – 14 – 36 = –26 4 a) –28 b) 345 c) –1750 d) –2800 e) –2100 f) 8700 5 a) Kommutativgesetz und Assoziativgesetz: (–0,62 + (–4,5)) + (–1,38) = ((–4,5) + (–0,62)) + (–1,38) = –4,5 + (–0,62 + (–1,38)) = –4,5 + (–2) = –6,5 b) Kommutativgesetz: 2 1 __ 3 + ( –5 ___ 8 ) – 7 __ 3 = 7 __ 3 – 7 __ 3 + ( –5 ___ 8 ) = – 5 __ 8 c) Kommutativgesetz: –4,5 + 8,23 – 15,5 = –4,5 – 15,5 + 8,23 = –20 + 8,23 = –11,77 d) Kommutativgesetz: – 1 __ 5 – ( 3 ___ –8 ) + 3 ___ 10 = – 1 __ 5 + 3 __ 8 + 3 ___ 10 = 3 __ 8 – 2 ___ 10 + 3 ___ 10 = 3 __ 8 + 1 ___ 10 = 15 + 4 _____40 = 19 ___ 40 6 7 a) Klammer ausrechnen, dann multiplizieren: ( – 3 __ 5 – 2 __ 5 ) · ( – 5 __ 6 ) = ( – 5 __ 5 ) · ( – 5 __ 6 ) = 5 __ 6 Distributivgesetz anwenden: ( – 3 __ 5 – 2 __ 5 ) · ( – 5 __ 6 ) = ( – 3 __ 5 ) · ( – 5 __ 6 ) + ( – 2 __ 5 ) · ( – 5 __ 6 ) = 3 __ 6 + 2 __ 6 = 5 __ 6 a) b) a b c a – (b – c) (a – b) – c 1 __ 2 1 __ 3 1 __ 6 1 __ 3 0 7 ___ 10 – 2 __ 5 1 __ 4 1 7 ___ 20 17 ___ 20 3 1 __ 4 –2 1 __ 4 –1 3 __ 8 4 1 __ 8 6 7 __ 8 + 0,34 2,8 3,45 3,79 6,25 2,647 2,987 5,447 3,012 3,352 5,812 – 1,56 0,563 12,34 10,78 11,777 3,172 1,612 2,609 5 3,44 4,437 a) 1,45 1,76 0,5 0,138 0,723 0,06 b) 2,552 2,9 3,52 0,099774 2,3 4,437 20° 75° 90° 135° 180° 210° 280° 3 __ 4 3 ___ 10 3 __ 5 3 ___ 20 1 ___ 20 2 ___ 15 3 __ 2 = 1 1 __ 2 3 __ 4 3 __ 5 1 ___ 12 1 __ 6 7 ___ 60 Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C . B uc hn er V er la gs