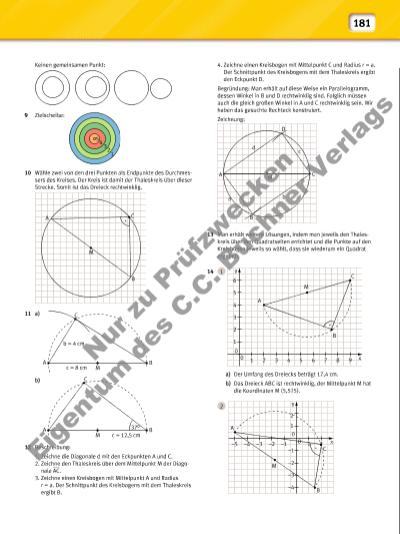
181 Keinen gemeinsamen Punkt: 9 Zielscheibe: 10 Wähle zwei von den drei Punkten als Endpunkte des Durchmessers des Kreises. Der Kreis ist damit der Thaleskreis über dieser Strecke. Somit ist das Dreieck rechtwinklig. 11 a) b) 12 Beschreibung: 1. Zeichne die Diagonale d mit den Eckpunkten A und C. 2. Zeichne den Thaleskreis über dem Mittelpunkt M der Diagonale ___ AC. 3. Zeichne einen Kreisbogen mit Mittelpunkt A und Radius r = a. Der Schnittpunkt des Kreisbogens mit dem Thaleskreis ergibt B. 4. Zeichne einen Kreisbogen mit Mittelpunkt C und Radius r = a. Der Schnittpunkt des Kreisbogens mit dem Thaleskreis ergibt den Eckpunkt D. Begründung: Man erhält auf diese Weise ein Parallelogramm, dessen Winkel in B und D rechtwinklig sind. Folglich müssen auch die gleich großen Winkel in A und C rechtwinklig sein. Wir haben das gesuchte Rechteck konstruiert. Zeichnung: 13 Man erhält weitere Lösungen, indem man jeweils den Thaleskreis über den Quadratseiten errichtet und die Punkte auf den Kreisbögen jeweils so wählt, dass sie wiederum ein Quadrat ergeben. 14 1 a) Der Umfang des Dreiecks beträgt 17,4 cm. b) Das Dreieck ABC ist rechtwinklig, der Mittelpunkt M hat die Koordinaten M (5,5 | 5). 2 1 2 3 4 5 M A C B A B C M b = 4 cm c = 8 cm A B C M c = 12,5 cm 37° 1 B 5 y x A 3 2 0 0 1 C 2 3 4 6 7 8 M 9 4 5 6 M 2 y x 0 0 –2 1 –1 –3 –2 1 2–1–3–4–5 A B C –4 A B C D M d a b c Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C . B uc hn er V er la gs