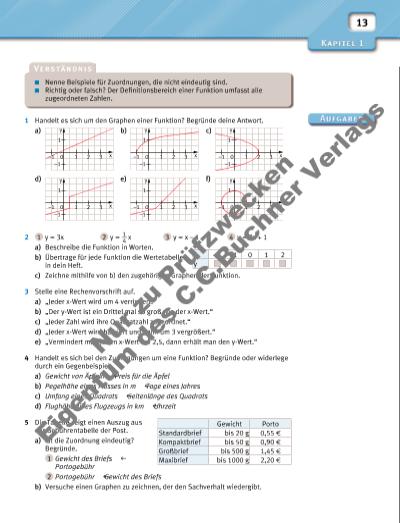
13 1 Handelt es sich um den Graphen einer Funktion? Begründe deine Antwort. a) b) c) d) e) f) 2 1 y = 3x 2 y = 1 __ 4 x 3 y = x – 1 4 y = 2x + 1 a) Beschreibe die Funktion in Worten. b) Übertrage für jede Funktion die Werte tabelle in dein Heft. c) Zeichne mithilfe von b) den zugehörigen Graphen der Funktion. 3 Stelle eine Rechenvorschrift auf. a) „Jeder x-Wert wird um 4 verringert.“ b) „Der y-Wert ist ein Drittel mal so groß wie der x-Wert.“ c) „Jeder Zahl wird ihre Quadratzahl zugeordnet.“ d) „Jeder x-Wert wird halbiert und dann um 3 vergrößert.“ e) „Vermindert man jeden x-Wert um 2,5, dann erhält man den y-Wert.“ 4 Handelt es sich bei den Zuordnungen um eine Funktion? Begründe oder widerlege durch ein Gegenbeispiel. a) Gewicht von Äpfeln g Preis für die Äpfel b) Pegelhöhe eines Flusses in m g Tage eines Jahres c) Umfang eines Quadrats g Seitenlänge des Quadrats d) Flughöhe eines Flugzeugs in km g Uhrzeit 5 Die Tabelle zeigt einen Auszug aus der Gebührentabelle der Post. a) Ist die Zuordnung eindeutig? Begründe. 1 Gewicht des Briefs g Portogebühr 2 Portogebühr g Gewicht des Briefs b) Versuche einen Graphen zu zeichnen, der den Sachverhalt wiedergibt. Nenne Beispiele für Zuordnungen, die nicht eindeutig sind. Richtig oder falsch? Der Defi nitionsbereich einer Funktion umfasst alle zugeordneten Zahlen. y x1 2 30 1 –1 –1 y x1 2 30 1 –1 –1 y x1 2 30 1 –1 –1 y x1 2 30 1 –1 –1 y x1 2 30 1 –1 –1 y x1 2 30 1 –1 –1 x –2 –1 0 1 2 y Gewicht Porto Standardbrief bis 20 g 0,55 f Kompaktbrief bis 50 g 0,90 f Großbrief bis 500 g 1,45 f Maxibrief bis 1000 g 2,20 f Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C .B uc hn er V er la gs