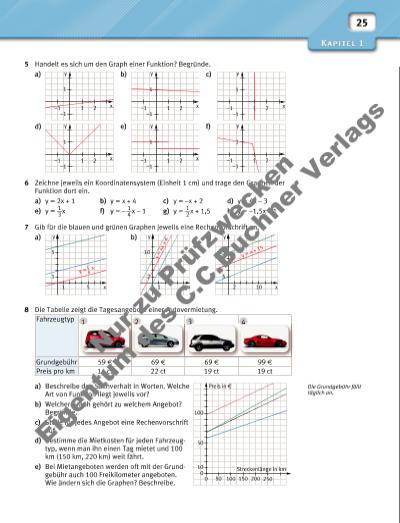
25 Die Grundgebühr fällt täglich an. 5 Handelt es sich um den Graph einer Funktion? Begründe. a) b) c) d) e) f) 6 Zeichne jeweils ein Koordinatensystem (Einheit 1 cm) und trage den Graphen der Funktion dort ein. a) y = 2x + 1 b) y = x + 4 c) y = –x + 2 d) y = 4x – 3 e) y = 1 __ 3 x f) y = – 1 __ 4 x – 1 g) y = 1 __ 2 x + 1,5 h) y = –1,5x – 1 7 Gib für die blauen und grünen Graphen jeweils eine Rechenvorschrift an. a) b) c) 8 Die Tabelle zeigt die Tagesangebote einer Autovermietung. a) Beschreibe den Sachverhalt in Worten. Welche Art von Funktion liegt jeweils vor? b) Welcher Graph gehört zu welchem Angebot? Begründe. c) Stelle für jedes Angebot eine Rechenvorschrift auf. d) Bestimme die Mietkosten für jeden Fahrzeugtyp, wenn man ihn einen Tag mietet und 100 km (150 km, 220 km) weit fährt. e) Bei Mietangeboten werden oft mit der Grundgebühr auch 100 Freikilometer angeboten. Wie ändern sich die Graphen? Beschreibe. Fahrzeugtyp 1 2 3 4 Grundgebühr 59 f 69 f 69 f 99 f Preis pro km 14 ct 22 ct 19 ct 19 ct y 2 10 5 25 x y = x + 1 5 y 1 5 1 5 x y = x1 4 y = 4 x + 4y 1 5 2 10 x Preis in f 0 50 100 150 200 250 0 10 50 100 Streckenlänge in km y x1–1 2 –1 1 y x1–1 2 –1 1 y x1–1 2 –1 1 y x1–1 2 –1 1 y x1–1 2 –1 1 y x1–1 2 –1 1 Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C .B uc hn er V er la gs