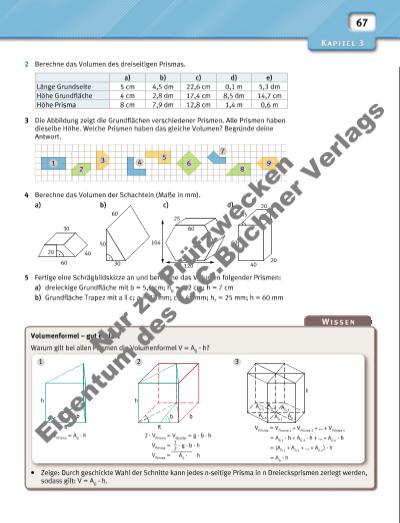
67 2 Berechne das Volumen des dreiseitigen Prismas. 3 Die Abbildung zeigt die Grundfl ächen verschiedener Prismen. Alle Prismen haben dieselbe Höhe. Welche Prismen haben das gleiche Volumen? Begründe deine Antwort. 4 Berechne das Volumen der Schachteln (Maße in mm). a) b) c) d) 5 Fertige eine Schrägbildskizze an und berechne das Volumen folgender Prismen: a) dreieckige Grundfl äche mit b = 5,6 cm; hb = 4,2 cm; h = 7 cm b) Grundfl äche Trapez mit a || c; a = 72 mm; c = 48 mm; hT = 25 mm; h = 60 mm a) b) c) d) e) Länge Grundseite 5 cm 4,5 dm 22,6 cm 0,1 m 5,3 dm Höhe Grundfl äche 4 cm 2,8 dm 17,4 cm 8,5 dm 14,7 cm Höhe Prisma 8 cm 7,9 dm 12,8 cm 1,4 m 0,6 m 1 53 8 9 2 7 4 6 60 30 120 40 104 60 20 50 30 60 25 60 45 20 20 40 1 2 3 h A G 1 A G 2 A G 3 A G 4AG 5 A G 6 h bb g h b g Volumenformel – gut erklärt Warum gilt bei allen Prismen die Volumenformel V = AG · h? • Zeige: Durch geschickte Wahl der Schnitte kann jedes n-seitige Prisma in n Dreiecksprismen zerlegt werden, sodass gilt: V = AG · h. VPrisma = AG · h VPrisma = VPrisma 1 + VPrisma 2 + … + VPrisma n = AG 1 · h + AG 2 · h + … + AG n · h = (AG 1 + AG 2 + … + AG n) · h = AG · h 2 · VPrisma = VQuader = g · b · h VPrisma = 1 __ 2 · g · b · h VPrisma = AG · h Nu r z u Pr üf zw ec ke n Ei en tu m d es C .C .B uc hn er V er la gs