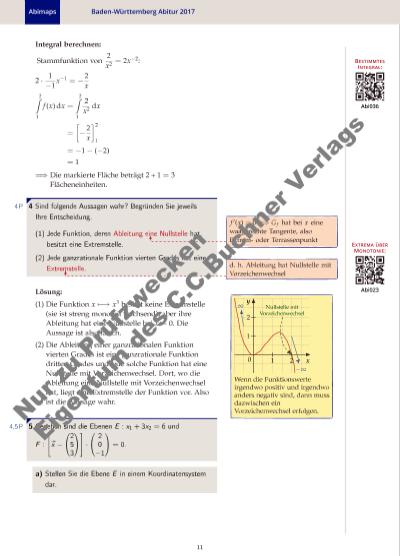
Abimaps Baden-Württemberg Abitur 2017 Integral berechnen: BESTIMMTESINTEGRAL: Abi036 Stammfunktion von 2 x2 = 2x−2: 2 · 1−1x −1 = −2 x 2∫ 1 f (x) dx = 2∫ 1 2 x2 dx = [ −2 x ]2 1 = −1− (−2) = 1 =⇒ Die markierte Fläche beträgt 2 + 1 = 3 Flächeneinheiten. 44P Sind folgende Aussagen wahr? Begründen Sie jeweils Ihre Entscheidung. (1) Jede Funktion, deren Ableitung eine Nullstelle hat, besitzt eine Extremstelle. EXTREMA U¨BERMONOTONIE: Abi023 f ′(x) = 0 =⇒ G f hat bei x eine waagerechte Tangente, also Extremoder Terrassenpunkt (2) Jede ganzrationale Funktion vierten Grades hat eine Extremstelle. d. h. Ableitung hat Nullstelle mit Vorzeichenwechsel Lösung: (1) Die Funktion x 7−→ x3 besitzt keine Extremstelle (sie ist streng monoton wachsend), aber ihre Ableitung hat eine Nullstelle bei x = 0. Die Aussage ist also falsch. (2) Die Ableitung einer ganzrationalen Funktion vierten Grades ist eine ganzrationale Funktion dritten Grades und jede solche Funktion hat eine Nullstelle mit Vorzeichenwechsel. Dort, wo die Ableitung eine Nullstelle mit Vorzeichenwechsel hat, liegt eine Extremstelle der Funktion vor. Also ist die Aussage wahr. 1 20 1 2 x y ∞ −∞ Nullstelle mit Vorzeichenwechsel VERANSCHAULICHUNG DER ABLEITUNG Wenn die Funktionswerte irgendwo positiv und irgendwo anders negativ sind, dann muss dazwischen ein Vorzeichenwechsel erfolgen. 54,5P Gegeben sind die Ebenen E : x1 + 3x2 = 6 und F : x − 25 3  ·  20 −1  = 0. a) Stellen Sie die Ebene E in einem Koordinatensystem dar. 11 Nu r z u Pr üf zw ec ke n Ei ge nt m d es C .C .B uc hn er V er la gs