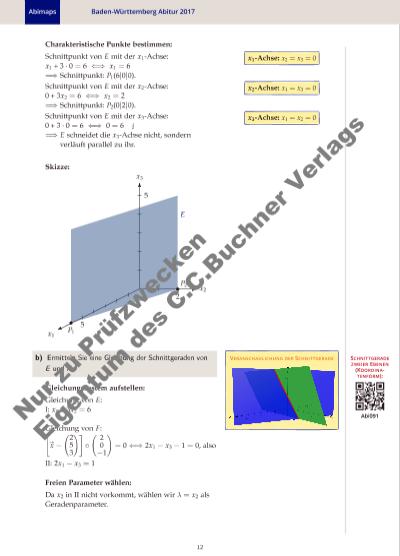
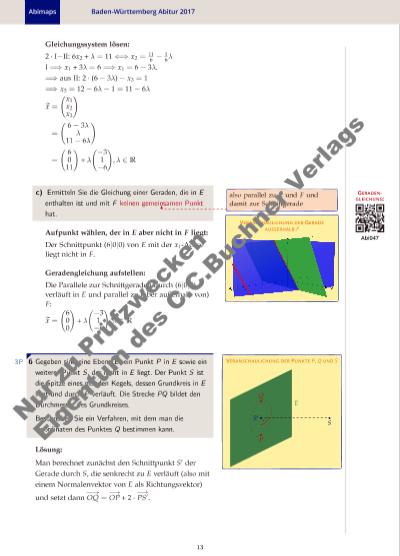
Abimaps Baden-Württemberg Abitur 2017 Gleichungssystem lösen: 2 · I−II: 6x2 + λ = 11⇐⇒ x2 = 116 − 16λ I =⇒ x1 + 3λ = 6 =⇒ x1 = 6− 3λ. =⇒ aus II: 2 · (6− 3λ)− x3 = 1 =⇒ x3 = 12− 6λ− 1 = 11− 6λ x = (x1 x2 x3 ) = ( 6− 3λ λ 11− 6λ ) = ( 6 0 11 ) + λ (−3 1 −6 ) ,λ ∈ R c) VERANSCHAULICHUNG DER GERADE AUSSERHALB F GERADENGLEICHUNG: Abi047 Ermitteln Sie die Gleichung einer Geraden, die in E enthalten ist und mit F keinen gemeinsamen Punkt hat. also parallel zu E und F und damit zur Schnittgerade Aufpunkt wählen, der in E aber nicht in F liegt: Der Schnittpunkt (6|0|0) von E mit der x1-Achse liegt nicht in F. Geradengleichung aufstellen: Die Parallele zur Schnittgeraden durch (6|0|0) verläuft in E und parallel zu (aber außerhalb von) F: x = ( 6 0 0 ) + λ (−3 1 −6 ) ,λ ∈ R 63P E P Q S S′ VERANSCHAULICHUNG DER PUNKTE P, Q UND SGegeben sind eine Ebene E , ein Punkt P in E sowie ein weiterer Punkt S , der nicht in E liegt. Der Punkt S ist die Spitze eines geraden Kegels, dessen Grundkreis in E liegt und durch P verläuft. Die Strecke PQ bildet den Durchmesser des Grundkreises. Beschreiben Sie ein Verfahren, mit dem man die Koordinaten des Punktes Q bestimmen kann. Lösung: Man berechnet zunächst den Schnittpunkt S′ der Gerade durch S, die senkrecht zu E verläuft (also mit einem Normalenvektor von E als Richtungsvektor) und setzt dann OQ = OP + 2 · PS′. 13 N r z u Pr üf zw ke n Ei ge nt um d es C .C .B uc hn er V er la gs