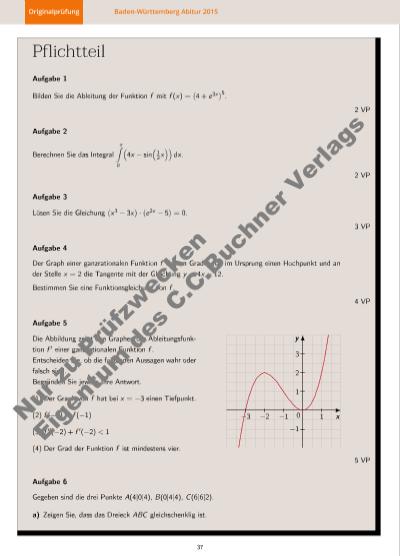
Originalprüfung Baden-Württemberg Abitur 2015 Pflichtteil Aufgabe 1 Bilden Sie die Ableitung der Funktion f mit f (x) = ( 4 + e3x )5. 2 VP Aufgabe 2 Berechnen Sie das Integral pi∫ 0 ( 4x − sin ( 1 2x )) dx . 2 VP Aufgabe 3 Lösen Sie die Gleichung ( x3 − 3x) · (e2x − 5) = 0. 3 VP Aufgabe 4 Der Graph einer ganzrationalen Funktion f dritten Grades hat im Ursprung einen Hochpunkt und an der Stelle x = 2 die Tangente mit der Gleichung y = 4x − 12. Bestimmen Sie eine Funktionsgleichung von f . 4 VP Aufgabe 5 Die Abbildung zeigt den Graphen der Ableitungsfunktion f ′ einer ganzrationalen Funktion f . Entscheiden Sie, ob die folgenden Aussagen wahr oder falsch sind. Begründen Sie jeweils Ihre Antwort. (1) Der Graph von f hat bei x = −3 einen Tiefpunkt. (2) f (−2) < f (−1) (3) f ′′(−2) + f ′(−2) < 1 (4) Der Grad der Funktion f ist mindestens vier. −3 −2 −1 10 −1 1 2 3 x y 5 VP Aufgabe 6 Gegeben sind die drei Punkte A(4|0|4), B(0|4|4), C (6|6|2). a) Zeigen Sie, dass das Dreieck ABC gleichschenklig ist. 37 Nu r z u Pr üf zw ec ke n Ei ge tu m d es C .C .B uc hn er V er la gs