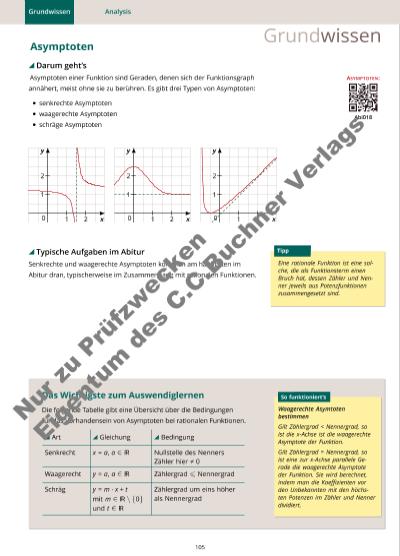
Grundwissen Analysis GrundwissenAsymptoten Darum geht’s ASYMPTOTEN: Abi018 Asymptoten einer Funktion sind Geraden, denen sich der Funktionsgraph annähert, meist ohne sie zu berühren. Es gibt drei Typen von Asymptoten: • senkrechte Asymptoten • waagerechte Asymptoten • schräge Asymptoten 1 20 1 2 x y senkrechte Asymptote 1 2 0 1 2 x y waagerechte Asymptote 1 2 0 1 2 x y schräge Asymptote Typische Aufgaben im Abitur Eine rationale Funktion ist eine sol-che, die als Funktionsterm einenBruch hat, dessen Zähler und Nen-ner jeweils aus Potenzfunktionenzusammengesetzt sind. Tipp Senkrechte und waagerechte Asymptoten kommen am häufigsten im Abitur dran, typischerweise im Zusammenhang mit rationalen Funktionen. Das Wichtigste zum Auswendiglernen Die folgende Tabelle gibt eine Übersicht über die Bedingungen für das Vorhandensein von Asymptoten bei rationalen Funktionen. Waagerechte Asymtotenbestimmen Gilt Zählergrad < Nennergrad, soist die x-Achse ist die waagerechteAsymptote der Funktion. Gilt Zählergrad = Nennergrad, soist eine zur x-Achse parallele Ge-rade die waagerechte Asymptoteder Funktion. Sie wird berechnet,indem man die Koeffizienten vorden Unbekannten mit den höchs-ten Potenzen im Zähler und Nennerdividiert. So funktioniert’s Art Gleichung Bedingung Senkrecht x = a, a ∈ R Nullstelle des Nenners Zähler hier 6= 0 Waagerecht y = a, a ∈ R Zählergrad 6 Nennergrad Schräg y = m · x + t mit m ∈ R \ {0} und t ∈ R Zählergrad um eins höher als Nennergrad 105 Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C .B uc hn er V er la gs